题目内容
如图所示,固定在竖直平面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接,轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1.现用一水平恒力F向右推物块,已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x.在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2,空气阻力不计.
(1)要使物块能够安全通过圆轨道的最高点D,求x的范围;
(2)在满足(1)问的情况下,在坐标系中作出压力传感器的读数FN与x的关系图象.

(1)要使物块能够安全通过圆轨道的最高点D,求x的范围;
(2)在满足(1)问的情况下,在坐标系中作出压力传感器的读数FN与x的关系图象.

分析:要清楚的知道物体通过圆形轨道最高点的最小速度.根据压力传感器所能承受的最大压力为90N,运用牛顿第二定律求出物体在最高点的最大速度.运用动能定理求出最大和最小速度两种情况下的C点到A点的距离.
也可以找到FN与x的关系,再从FN的范围求出x的范围.
也可以找到FN与x的关系,再从FN的范围求出x的范围.
解答: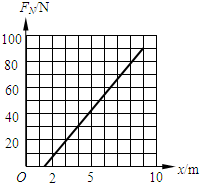 解:(1)A到B过程,由得动能定理得:
解:(1)A到B过程,由得动能定理得:
Fx-μmgL=
mvB2
B到D过程,由动能定理得:
-2mgR=
mvD2-
mvB2
物块到达D点时,由牛顿第二定律得:
FN+mg=m
由以上三式得:
FN=
-5mg
FN=12x-18
∵0≤FN≤90N
解得:1.5m≤x≤9m
(2)根据表达式FN=12x-18,取特殊点作图.
答:(1)x的范围是1.5m≤x≤9m
(2)见上图.
 解:(1)A到B过程,由得动能定理得:
解:(1)A到B过程,由得动能定理得:Fx-μmgL=
| 1 |
| 2 |
B到D过程,由动能定理得:
-2mgR=
| 1 |
| 2 |
| 1 |
| 2 |
物块到达D点时,由牛顿第二定律得:
FN+mg=m
| ||
| R |
由以上三式得:
FN=
| 2(Fx-μmgL) |
| R |
FN=12x-18
∵0≤FN≤90N
解得:1.5m≤x≤9m
(2)根据表达式FN=12x-18,取特殊点作图.
答:(1)x的范围是1.5m≤x≤9m
(2)见上图.
点评:动能定理的应用范围很广,能够求解的物理量也很多,有许多物理量含在某个物理量的表达式里面.
该题的突破口是要运用动能定理找到FN与x的关系,再从FN的范围求出x的范围.
我们在读题时要抓住题目的一些关键语言,这可能就是突破口.
该题的突破口是要运用动能定理找到FN与x的关系,再从FN的范围求出x的范围.
我们在读题时要抓住题目的一些关键语言,这可能就是突破口.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图所示,固定在竖直平面半径为R的光滑圆环,有质量为m的小球在轨道内侧作圆周运动,小球恰好能通过圆环的最高点.已知重力加速度为g,则小球在运动过程( )
如图所示,固定在竖直平面半径为R的光滑圆环,有质量为m的小球在轨道内侧作圆周运动,小球恰好能通过圆环的最高点.已知重力加速度为g,则小球在运动过程( ) 如图所示,固定在竖直平板且不可伸长的绝缘轻绳栓一质量为m、电量为q的小球(可视为点电荷),小球平衡时与固定在平板的点电荷Q的连线恰好水平.若小球的质量变为2m时,而其位置仍要保持不变,则小球的电量应该变为
如图所示,固定在竖直平板且不可伸长的绝缘轻绳栓一质量为m、电量为q的小球(可视为点电荷),小球平衡时与固定在平板的点电荷Q的连线恰好水平.若小球的质量变为2m时,而其位置仍要保持不变,则小球的电量应该变为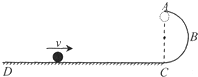 计,g取10m/s2.
计,g取10m/s2.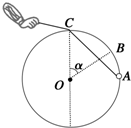 如图所示,固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔,一质量为m=0.1kg的小球套在圆环上,一根细线的一端拴着这个小球,细线的另一端穿过小孔C,手拉细线使小球从A处沿圆环向上移动.在下列两种情况下,当小球通过B处,即∠COB=α=740时,求这两种情况下,细线对小球的拉力F的大小和圆环对小球的弹力FN的大小.(不计空气阻力,g取10m/s2;sin37°=0.6,cos37°=0.8;可能用到
如图所示,固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔,一质量为m=0.1kg的小球套在圆环上,一根细线的一端拴着这个小球,细线的另一端穿过小孔C,手拉细线使小球从A处沿圆环向上移动.在下列两种情况下,当小球通过B处,即∠COB=α=740时,求这两种情况下,细线对小球的拉力F的大小和圆环对小球的弹力FN的大小.(不计空气阻力,g取10m/s2;sin37°=0.6,cos37°=0.8;可能用到