题目内容
【题目】如图所示,质量m=1kg的小球(可看成质点),从距离一固定于水平面的半圆形槽上沿高H=5m处自由下落,接着沿半圆形槽壁运动,半圆槽半径R=0.5m。小球第一次到达槽最低点时速率为10m/s,并继续沿槽壁运动直到从槽左端边缘飞出,如此反复几次,设摩擦力大小恒定不变,小球与槽壁相碰时不损失能量,不计空气阻力,求:(取g=10m/s2)
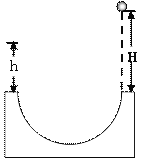
(1)从开始直到小球停止运动过程中,克服摩擦力做的功;
(2)小球第一次离槽上升距槽上沿的高度h。
【答案】(1)55J;(2)4m
【解析】
(1)对开始直到小球停止运动的全过程应用动能定理,可得全过程中摩擦力做的功,进而求得全过程中小球克服摩擦力做的功。
(2)因摩擦力大小不变,小球从出发到第一次离槽到达最高点过程中摩擦力做的功是小球从出发到第一次到达槽最低点摩擦力做功的两倍;对这两个过程分别应用动能定理可求得小球第一次离槽上升距槽上沿的高度。
(1)小球最后停在槽底,对整个过程应用动能定理,则:
![]() ,即
,即![]()
解得![]()
(2)设小球从出发到第一次到达槽最低点过程中,摩擦力做的功为![]() ,则
,则
小球从出发到第一次到达槽最低点![]()
小球从出发到第一次离槽到达最高点![]()
联立可得![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
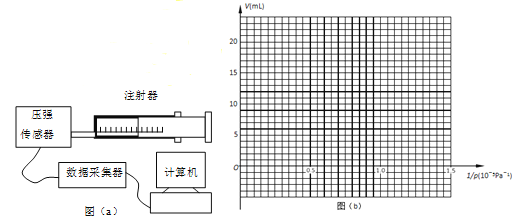
【题目】用DIS研究一定质量气体在温度不变时,压强与体积关系的实验装置如图![]() 。
。
![]() 实验中,不能用手握住注射器封闭气体部分,是为了保持______;
实验中,不能用手握住注射器封闭气体部分,是为了保持______;
![]() 移动活塞,输入气体体积V,同时计算机记录对应的气体压强值p,实验数据如下表所示:
移动活塞,输入气体体积V,同时计算机记录对应的气体压强值p,实验数据如下表所示:
实验次序 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
| 10 | 12 | 14 | 16 | 18 | 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
观察发现![]() 一栏中的数值越来越大,为了研究造成这一现象的可能原因,在图
一栏中的数值越来越大,为了研究造成这一现象的可能原因,在图![]() 中画出
中画出![]() 图象____________;
图象____________;
![]() 如果实验操作规范正确,从图象中可以判断表格中哪一栏数据记录有误,并说明如何修正:______。
如果实验操作规范正确,从图象中可以判断表格中哪一栏数据记录有误,并说明如何修正:______。