题目内容
【题目】如图所示，OA为一遵守胡克定律的弹性轻绳，其一端固定在天花板上的O点，另一端与静止在动摩擦因数恒定的水平地面上的滑块A相连．当绳处于竖直位置时，滑块A与地面有压力作用．B为一紧挨绳的光滑水平小钉，它到天花板的距离BO等于弹性绳的自然长度．现用水平力F作用于A，使之向右作直线运动，在运动过程中，作用于A的摩擦力（ ）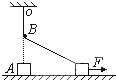
A.逐渐增大
B.逐渐减小
C.保持不变
D.条件不足，无法判断
【答案】C
【解析】解：
滑块在A点时，受到向下的重力mg、地面的支持力 
、绳子的拉力F=k 
，且有mg=k 
，解得 =mg﹣k
当滑块运动到图示位置C时（设弹性绳与竖直方向夹角为θ），受力分析如图所示：
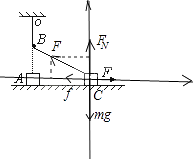
由滑块在竖直方向受到的合力为零可得：mg= 
+k 
cosθ，由图可知 
= ，解 = ，即滑块受到地面的弹力不变，由f=μ 知，作用于A的摩擦力不变，所以C正确ABD错误．
故选：C．
【考点精析】认真审题，首先需要了解滑动摩擦力(滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解)．
愉快的寒假南京出版社系列答案
【题目】在“探究加速度与力、质量的关系”的实验中，采用如图1所示的装置．
①本实验应用的实验方法是；
②下列说法中正确的是
A．在探究加速度与质量的关系时，应改变拉力的大小；
B．在探究加速度与外力的关系时，应该改变小车的质量；
C．在探究加速度a与质量m的关系时，为了直观判断二者间的关系，应作出a﹣ 
图象；
D．当小车的质量远大于砝码盘和砝码的总质量时，才能近似认为细线对小车的拉力大小等于砝码盘和砝码的总重力大小．
③某同学测得小车的加速度a和拉力F的数据如表所示：（小车质量保持不变．）
F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
a/ms﹣2 | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
A．根据表中的数据在坐标图2上作出a﹣F图象 ．
B．图线不过原点的原因可能是
