题目内容
14.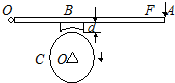 如图,杆长OA=0.5米,O端用铰链铰于竖直墙面,杆中B处有一制动闸,OB=0.2米,闸厚d=0.04米,轮子C的半径为R=0.2米,闸与轮间摩擦系数为μ=0.5,当飞轮顺时针转动对轮施加力矩M=1000牛米才能使轮减速而制动,若杆与闸的重力不计,则在杆的A端需加垂直于杆的力F的大小为4000牛.
如图,杆长OA=0.5米,O端用铰链铰于竖直墙面,杆中B处有一制动闸,OB=0.2米,闸厚d=0.04米,轮子C的半径为R=0.2米,闸与轮间摩擦系数为μ=0.5,当飞轮顺时针转动对轮施加力矩M=1000牛米才能使轮减速而制动,若杆与闸的重力不计,则在杆的A端需加垂直于杆的力F的大小为4000牛.
分析 根据使轮减速而制动的力矩和轮子C的半径求出使轮减速制动需要的摩擦力,根据动摩擦因数求出作用在B上的压力F2,最后根据杠杆平衡条件求出作用在A的动力F.
解答 解:能使轮减速而制动时对轮施加力矩为1000牛米,即fR=1000N•m,
得:f=$\frac{1000N•m}{0.2m}$=5000N.
闸与轮间动摩擦因数μ为0.5,
由f=μN得:N=F2=$\frac{f}{μ}$=$\frac{5000N}{0.5}$=10000N,
根据杠杆平衡条件得:FOA=F2OB,
F=$\frac{\left.\begin{array}{l}{{F}_{2}OB}\end{array}\right.}{OA}$=$\frac{10000N×0.2m}{0.5m}$=4000N.
故答案为:4000.
点评 本题考查力矩、动摩擦因数和杠杆平衡条件的应用,关键是理解力矩的物理意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法正确的是( )
| A. | 电荷量很小的点电荷称元电荷 | |
| B. | 一个带电体的电荷量可以为元电荷的205.5倍 | |
| C. | 元电荷是最小的电荷量 | |
| D. | 元电荷没有正、负之分 |
2.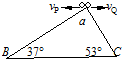 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )| A. | 16:9 | B. | 9:16 | C. | 1:1 | D. | 4:3 |
9.小球作类平抛运动时,分在两个互相垂直方向上的分运动的图线可能是( )


| A. | a和b | B. | b和d | C. | a和d | D. | c和d |
6.在光滑绝缘的水平面上有一个不导电的弹簧,弹簧的两端分别与金属小球A、B相连,若A、B带上等量同种电荷,弹簧伸长x1,若让A、B所带电量都增为原来的2倍,弹簧的伸长量为x2,则x1与x2的关系是( )
| A. | x2=x1 | B. | x2=4x1 | C. | x2>4x1 | D. | x2<4x1 |
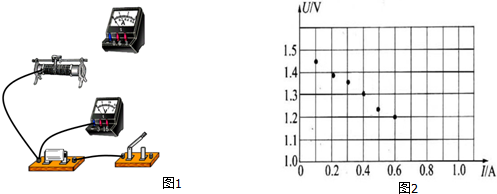
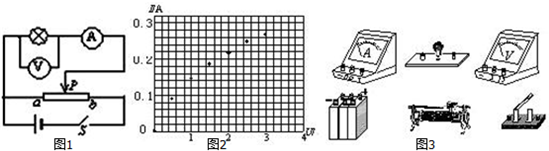
 如图所示O、A、B为平抛物体的运动轨迹上的三个点(O点不是平抛起始点),平抛物体的初速度v0=$\sqrt{2}$m/s(g=10m/s2)
如图所示O、A、B为平抛物体的运动轨迹上的三个点(O点不是平抛起始点),平抛物体的初速度v0=$\sqrt{2}$m/s(g=10m/s2) 如图所示是某矿井中的升降机由井底到井口运动的图象,试根据图象分析回答:0~2s,加速度是6m/s2;4s~5s,加速度是-12 m/s2,在这个时间内升降机是在做匀减直线运动(填“加”或“减”); 这口矿井的深度为42 m.
如图所示是某矿井中的升降机由井底到井口运动的图象,试根据图象分析回答:0~2s,加速度是6m/s2;4s~5s,加速度是-12 m/s2,在这个时间内升降机是在做匀减直线运动(填“加”或“减”); 这口矿井的深度为42 m.