题目内容
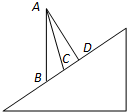如图所示在倾斜角为θ的斜面上方的A点处放置光滑板AB、AC、AD各端点刚好在斜面上，AB竖直，AD⊥BD，AC为∠BAD的角分线，一质点自A端由静止滑到B端的时间为tB，滑到C端的时间为tC，滑到D端的时间为tD，则（ ）| A、tC最小，tB≠tD | B、tB最小，tC≠tD | C、tC最小，tB=tD | D、tD最小，tC≠tB |
分析：AB竖直，AD⊥BD，以AB为直径画圆必定过D点，根据等时圆的结论及几何关系即可求解．
解答：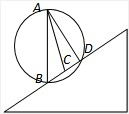
解：如图所示：AB竖直，AD⊥BD，以AB为直径画圆必定过D点，
设小物块下滑的轨道与竖直方向的夹角为θ，圆的半径为R，根据牛顿第二定律得，a=
=gcosθ
轨道的位移x=2Rcosθ．
根据2Rcosθ=
at2
解得：t=
与θ角无关．
所以从A点滑到圆上任一点的时间都相等，则由A点滑到D点所用时间和A点滑到B点所需时间相等，
即tB=tD
AC的长度比从A沿AC方向到达圆周的长度小，所以时间也短，即tC最小，
故选：C
解：如图所示：AB竖直，AD⊥BD，以AB为直径画圆必定过D点，设小物块下滑的轨道与竖直方向的夹角为θ，圆的半径为R，根据牛顿第二定律得，a=
| mgcosθ |
| m |
轨道的位移x=2Rcosθ．
根据2Rcosθ=
| 1 |
| 2 |
解得：t=
|
所以从A点滑到圆上任一点的时间都相等，则由A点滑到D点所用时间和A点滑到B点所需时间相等，
即tB=tD
AC的长度比从A沿AC方向到达圆周的长度小，所以时间也短，即tC最小，
故选：C
点评：本题有其特殊的解题方法，作等时圆是一种快捷、方便的方法，难道适中．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，BC为半径等于
如图所示，质量为m物块A在质量为M斜面B上正在以加速度a加速下滑，已知斜面倾斜角为θ，物块下滑过程中斜面始终静止，则下列说法中正确的是（ ）
如图所示，质量为M=6.0kg的物体A和质量为m=2.0kg的物体B，通过轻绳子跨过滑轮相连．斜面光滑且足够长，倾斜角θ=30°．不计绳子和滑轮之间的摩擦．开始时A物体在斜面上方，B物体位于水平地面上，用手托住A物体，A、B两物均静止．撤去手后，求：