题目内容
 如图所示,BC为半径等于
如图所示,BC为半径等于| 2 |
| 5 |
| 2 |
(1)小球从O点的正上方某处A点水平抛出的初速度v0为多少?
(2)小球在圆管中运动时对圆管的压力是多少?
(3)小球在CD斜面上运动的最大位移是多少?
分析:(1)小球从A运动到B为平抛运动,根据平抛运动的规律及几何关系求解初速度;
(2)小球从B到O过程力F和重力平衡,做匀速圆周运动;先求出B点的速度,根据向心力公式求解细管对小球的作用力;
(3)对从C到D过程,先受力分析,根据牛顿第二定律求解出加速度;然后运用运动学公式求解位移.
(2)小球从B到O过程力F和重力平衡,做匀速圆周运动;先求出B点的速度,根据向心力公式求解细管对小球的作用力;
(3)对从C到D过程,先受力分析,根据牛顿第二定律求解出加速度;然后运用运动学公式求解位移.
解答:解:(1)小球从A运动到B为平抛运动,有:
rsin45°=v0t
在B点,有:tan45°=
解以上两式得:v0=2m/s
(2)在B点据平抛运动的速度规律有:vB=
=2
m/s
小球在管中的受力分析为三个力:由于重力与外加的力F平衡,故小球所受的合力仅为管的外轨对它的压力,得小球在管中做匀速圆周运动,由圆周运动的规律得细管对小球的作用力N=m
=
N
根据牛顿第三定律得小球对细管的压力N′=N=5
N;
(3)在CD上滑行到最高点过程,根据牛顿第二定律得:
mgsin45°+μmgcos45°=ma
解得:a=g(sin45°+μcos45°)=8
m/s2
根据速度位移关系公式,有:
x=
=
m=
m;
答:(1)小球从O点的正上方某处A点水平抛出的初速度v0为2m/s;
(2)小球在圆管中运动时对圆管的压力是5
N;
(3)小球在CD斜面上运动的最大位移是
m.
rsin45°=v0t
在B点,有:tan45°=
| gt |
| v0 |
解以上两式得:v0=2m/s
(2)在B点据平抛运动的速度规律有:vB=
| v0 |
| sin45° |
| 2 |
小球在管中的受力分析为三个力:由于重力与外加的力F平衡,故小球所受的合力仅为管的外轨对它的压力,得小球在管中做匀速圆周运动,由圆周运动的规律得细管对小球的作用力N=m
| ||
| r |
| 2 |
根据牛顿第三定律得小球对细管的压力N′=N=5
| 2 |
(3)在CD上滑行到最高点过程,根据牛顿第二定律得:
mgsin45°+μmgcos45°=ma
解得:a=g(sin45°+μcos45°)=8
| 2 |
根据速度位移关系公式,有:
x=
| ||
| 2a |
| 8 | ||
2×8
|
| ||
| 4 |
答:(1)小球从O点的正上方某处A点水平抛出的初速度v0为2m/s;
(2)小球在圆管中运动时对圆管的压力是5
| 2 |
(3)小球在CD斜面上运动的最大位移是
| ||
| 4 |
点评:本题主要考查了平抛运动的基本规律及向心力公式的应用,解题时注意结合几何关系,难度适中.

练习册系列答案
相关题目
 (2011?顺德区模拟)如图所示,BC为半径等于R=
(2011?顺德区模拟)如图所示,BC为半径等于R=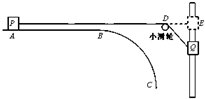 如图所示,BC为半径R=0.144m的
如图所示,BC为半径R=0.144m的