题目内容
 如图所示,BC为半径等于
如图所示,BC为半径等于| 2 |
| 5 |
| 2 |
| 2 |
(1)小球从O点的正上方某处A点水平抛出的初速度v0为多少?
(2)小球在从A点抛出到达到CD最高点的总时间?(结果保留两位有效数字)
(3)判断小球能否停在斜面上?若能请计算出所停的位置;若不能则请计算出此后通过C点时小球对圆管的最大压力的大小.
分析:(1)小球从A运动到B做平抛运动,根据平抛运动的基本公式及几何关系即可求得初速度;
(2)小球从进入圆管开始受到始终竖直向上的力F=5N的作用,跟重力恰好平衡,说明小球在圆管中做匀速圆周运动.分三段分别求出时间,即可求出总时间;
(3)判断小球能否停在斜面上,关键看重力沿斜面的分量跟滑动摩擦力的大小,如果重力沿斜面的分量大于滑动摩擦力,则不能静止,由向心力公式即可求出压力.
(2)小球从进入圆管开始受到始终竖直向上的力F=5N的作用,跟重力恰好平衡,说明小球在圆管中做匀速圆周运动.分三段分别求出时间,即可求出总时间;
(3)判断小球能否停在斜面上,关键看重力沿斜面的分量跟滑动摩擦力的大小,如果重力沿斜面的分量大于滑动摩擦力,则不能静止,由向心力公式即可求出压力.
解答:解:(1)小球从A运动到B为平抛运动,有:
rsin45°=v0t-------①
在B点有:tan45°=
-------②
解以上两式得:v0=2m/s
(2)在B点由运动的合成与分解有:
vB=
=2
m/s-------③
平抛运动A到B的时间为t1,则
Rsin45°=v0t1-------④
小球在管中受三个力作用,则小球在管中以vB=2
m/s做匀速圆周运动B到C时间为t2,故
πR=vBt2-------⑤
在CD上滑行到最高点时间为t3 根据牛顿第二定律得小球在斜面上滑的加速度为a1则mgsin45°+μmgcos45°=ma1------⑥
由匀变速运动规律得:vc=vB=a1t3-------⑦
由③④⑤⑥⑦联立得:t=t1+t2+t3=0.92s
(3)因为μ<tanθ,故小球不能停止在斜面上
根据牛顿第二定律得小球在斜面下滑的加速度为a2则mgsin45°-μmgcos45°=ma2------⑧
当小球第一次回到c点时对轨道的压力最大,设此时的速度为
由运动学规律有
=
-------⑨
在C点由牛顿第二定律得N-mg=m
-------⑩
由⑧⑨⑩联立得:N=6.75N
答:(1)小球从O点的正上方某处A点水平抛出的初速度为2m/s;
(2)小球在从A点抛出到达到CD最高点的总时间为0.92s;
(3)小球不能停止在斜面上,小球通过C点时对圆管的最大压力为6.75N.
rsin45°=v0t-------①
在B点有:tan45°=
| gt |
| v0 |
解以上两式得:v0=2m/s
(2)在B点由运动的合成与分解有:
vB=
| v0 |
| sin45° |
| 2 |
平抛运动A到B的时间为t1,则
Rsin45°=v0t1-------④
小球在管中受三个力作用,则小球在管中以vB=2
| 2 |
| 3 |
| 4 |
在CD上滑行到最高点时间为t3 根据牛顿第二定律得小球在斜面上滑的加速度为a1则mgsin45°+μmgcos45°=ma1------⑥
由匀变速运动规律得:vc=vB=a1t3-------⑦
由③④⑤⑥⑦联立得:t=t1+t2+t3=0.92s
(3)因为μ<tanθ,故小球不能停止在斜面上
根据牛顿第二定律得小球在斜面下滑的加速度为a2则mgsin45°-μmgcos45°=ma2------⑧
当小球第一次回到c点时对轨道的压力最大,设此时的速度为
| v | ′ C |
| ||
| 2a1 |
| v′C2 |
| 2a2 |
在C点由牛顿第二定律得N-mg=m
| v′C2 |
| R |
由⑧⑨⑩联立得:N=6.75N
答:(1)小球从O点的正上方某处A点水平抛出的初速度为2m/s;
(2)小球在从A点抛出到达到CD最高点的总时间为0.92s;
(3)小球不能停止在斜面上,小球通过C点时对圆管的最大压力为6.75N.
点评:本题主要考查了牛顿第二定律及平抛运动基本公式的应用,要求同学们能正确对物体进行受力分析,根据受力情况判断运动情况,并熟练运用运动学基本公式解题.

练习册系列答案
相关题目
 (2011?顺德区模拟)如图所示,BC为半径等于R=
(2011?顺德区模拟)如图所示,BC为半径等于R=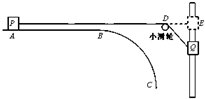 如图所示,BC为半径R=0.144m的
如图所示,BC为半径R=0.144m的