题目内容
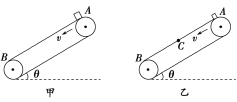
【题目】如图所示，甲、乙传送带倾斜于水平地面放置，并以相同的恒定速率v逆时针运动，两传送带粗糙程度不同，但长度、倾角均相同．将一小物体分别从两传送带顶端的A点无初速度释放，甲传送带上物体到达底端B点时恰好达到速度v；乙传送带上物体到达传送带中部的C点时恰好达到速度v，接着以速度v运动到底端B点．则物体从A运动到B的过程中( )
A．物体在甲传送带上运动的时间比乙大
B．物体与甲传送带之间的动摩擦因数比乙大
C．两传送带对物体做功相等
D．两传送带因与物体摩擦产生的热量相等
【答案】AC
【解析】物体在甲传送带上的平均速度为
，在乙传送带上的平均速度大于，而运动的位移相同，故物体在甲传送带上运动的时间比乙大，选项A正确；物体在甲传送带上加速距离比在乙传送带上加速距离大，而末速度相同，由v＝at可知a甲<a乙，由牛顿第二定律有μmgcos θ＋mgsin θ＝ma，故μ甲<μ乙，选项B错误；物体在运动过程中受重力和传送带的作用力，物体下降的高度和末速度均相等，由动能定理可知，传送带对物体做功相等，选项C正确；设传送带的高度为h，由摩擦生热Q＝fs相对知，Q甲＝f1s1＝f1(vt1－t1)＝f1·
，Q乙＝f2s2＝f2·
，根据牛顿第二定律得f1＋mgsin θ＝ma1＝m
，f2＋mgsin θ＝ma2＝m
，解得Q甲＝
mv2－mgh，Q乙＝mv2－mg(h－h′)，故Q甲<Q乙，选项D错误．
练习册系列答案
相关题目
