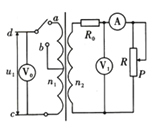
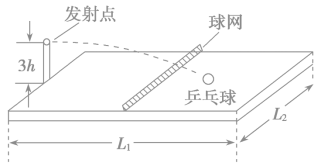
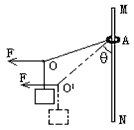
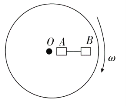
题目内容
【题目】如图所示,质量为m的小球从四分之一光滑圆弧轨道顶端静止释放,从轨道末端O点水平抛出,击中平台右下侧挡板上的P点。以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程y=6-x2(单位:m),小球质量m=0.4 kg,圆弧轨道半径R=1.25 m,g取10 m/s2;求:

(1)小球对圆弧轨道末端的压力大小;
(2)小球从O点到P点所需的时间(结果可保留根号)。
【答案】(1)12 N (2)![]() s
s
【解析】(1) 对小球,从释放到O点过程中
由机械能守恒:mgR=![]() mv2
mv2
v=![]() =
=![]() m/s=5 m/s
m/s=5 m/s
小球在圆轨道最低点:FN-mg=m![]()
FN=mg+m![]() =12 N
=12 N
由牛顿第三定律,小球对轨道的压力FN′=FN=12 N。
(2)小球从O点水平抛出后满足
y=![]() gt2
gt2
x=vt
又有y=6-x2
联立得t=![]() s。
s。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目