Question

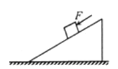
【题目】如图所示，质量为M的斜面体静止在粗糙的水平地面上，一质量为m的滑块沿斜面匀加速下滑，斜面体对地面压力为F1；现施加一平行斜面向下的推力F作用于滑块，在物块沿斜面下滑的过程中，斜面体对地面压力为F2。则

A.F2>(M+m)g, F2> F1

B.F2>(M+m)g, F2= F1

C.F2<(M+m)g, F2> F1

D.F2<(M+m)g, F2= F1

Answer 1

【答案】D

【解析】

当不受外力时，对m受力分析，由牛顿第二定律可得，

mgsinθ-f=ma1；

将加速度向水平和竖直方向分解，则竖直方向加速度

ay1=a1sinθ；

则对整体竖直方向有：

Mg+mg-F1=may1；

F1=Mg+mg-may=Mg+mg-（mgsinθ-f）sinθ：

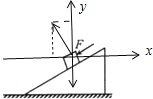
当加推力F后，对m有

F+mgsinθ-f=ma2

加速度的竖直分量

ay2=a2sinθ

则对整体有

Mg+mg+Fsinθ-F2=may2；

解得

F2=Mg+mg-（mgsinθ-f）sinθ

则可知

F1=F2＜（M+m）g

A．F2>(M+m)g，F2> F1，与结论不相符，选项A错误；

B．F2>(M+m)g，F2= F1，与结论不相符，选项B错误；

C．F2<(M+m)g， F2> F1，与结论不相符，选项C错误；

D．F2<(M+m)g，F2= F1，与结论相符，选项D正确；

故选D.