Question

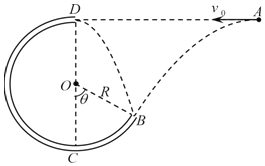
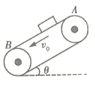
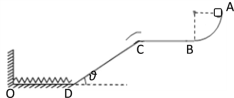
【题目】如图，质量为的小滑块（视为质点）在半径为的圆弧端由静止开始释放，它运动到点时速度为。当滑块经过后立即将圆弧轨道撤去。滑块在光滑水平面上运动一段距离后，通过换向轨道由点过渡到倾角为、长的斜面上，之间铺了一层匀质特殊材料，其与滑块间的动摩擦系数可在之间调节。斜面底部点与光滑地面平滑相连，地面上一根轻弹簧一端固定在点，自然状态下另一端恰好在点。认为滑块通过和前后速度大小不变，最大静摩擦力等于滑动摩擦力。取，，，不计空气阻力。

（1）求滑块对点的压力大小以及在上克服阻力所做的功；

（2）若设置，求质点从运动到的时间；

（3）若最终滑块停在点，求的取值范围。

Answer 1

【答案】（1）（2）（3） 或

【解析】

（1）根据牛顿第二定律求出滑块在B点所受的支持力，从而得出滑块对B点的压力，根据动能定理求出AB端克服阻力做功的大小；
（2）若μ=0，根据牛顿第二定律求出加速度，结合位移时间公式求出C到D的时间；
（3）最终滑块停在D点有两种可能，一个是滑块恰好从C下滑到D，另一种是在斜面CD和水平面见多次反复运动，最终静止在D点，结合动能定理进行求解；

（1）在点根据牛顿第二定律得到：，解得

由牛顿第三定律得到对B点的压力大小为：，方向竖直向下

从到，由动能定理得到：

得到：；

（2）在间运动，根据牛顿第二定律有：

则加速度大小为：

根据位移与时间的关系： 代入数据可以得到：；

（3）最终滑块停在点有两种可能：

、滑块恰好能从下滑到。

则根据动能定理：，可以得到：；

、滑块在斜面和水平地面间多次反复运动，最终静止于点。

当滑块恰好能返回：

得到

当滑块恰好能静止在斜面上，则有，得到

所以，当，滑块在和水平地面间多次反复运动，最终静止于点。

综上所述，的取值范围是 或。