题目内容
船在静水中的速度为v,流水的速度为u,河宽为L。
(1)为使渡河时间最短,应向什么方向划船?此时渡河所经历的时间和所通过的路程各为多大?
(2)为使渡河通过的路程最短,应向什么方向划船?此时渡河所经历的时间和所通过的路程各为多大?
(1)为使渡河时间最短,应向什么方向划船?此时渡河所经历的时间和所通过的路程各为多大?
(2)为使渡河通过的路程最短,应向什么方向划船?此时渡河所经历的时间和所通过的路程各为多大?
(1)应沿垂直于河岸的方向划船
 ,
,
(2)①当v>u时,划船的速度方向与河岸夹α角偏向上游方向
 ,合速度方向垂直于河岸。
,合速度方向垂直于河岸。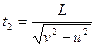 ,d2=L
,d2=L②当v<u时,划船的速度方向与河岸夹β角偏向上游方向
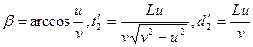
(1)为使渡河时间最短,必须使垂直于河岸的分速度尽可能大,即应沿
垂直于河岸的方向划船,此时所渡河经历的时间和通过的路程分别为
 ,
,
(2)为使渡河路程最短,必须使船的合速度方向尽可能垂直于河岸。分如下两种情况讨论:
①当v>u时,划船的速度方向与河岸夹α角偏向上游方向,合速度方向垂直于河岸。于是有

vcosα="u "
L=vsinαt2
d2=L
由此解得:
 ,
,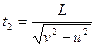 ,d2=L
,d2=L②当v<u时,划船的速度方向与河岸夹β角偏向上游方向,于是又有

 ,
,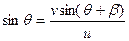
为使渡河路程最短,必须使船的合速度方向跟河岸的夹角最大,sin(β+θ)=π/2 , 即v垂直于v合
ucosβ="v "
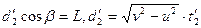
由此解
得:
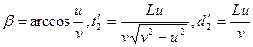

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
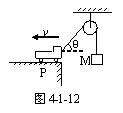



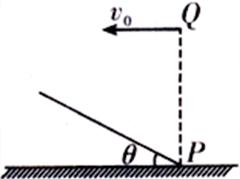
 的斜坡,在斜坡底端P点正上方的某一点Q处以速度
的斜坡,在斜坡底端P点正上方的某一点Q处以速度 水平向左抛出一个小球A,同时从Q由静止释放另一小球B. 已知小球A恰好垂直落在斜坡上,不计空气阻力,求:
水平向左抛出一个小球A,同时从Q由静止释放另一小球B. 已知小球A恰好垂直落在斜坡上,不计空气阻力,求: