题目内容
18.用如图所示的实验装置验证机械能守恒定律.(1)下面列举了该实验的几个操作步骤:
A.按照图1示的装置安装器件;
B.将打点计时器接到学生电源的“直流输出”上;
C.用天平测出重锤的质量;
D.先接通电源,后释放纸带,打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能.
其中没有必要进行的步骤是C,操作不当的步骤是BD.
(2)在用打点计时器验证机械能守恒定律的实验中(图2),重物质量m=1.00kg,如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置选取的三个连续点(其他点未画出).已知打点周期T=0.02s,当地的重力加速度g=9.80m/s2.试求:

①与重物相连接的是纸带的左端(选填“左”或“右”).
②根据图上所得数据,应取图中O点和B点来验证机械能守恒定律.
③从O点到所取点,重物重力势能的减小量△Ep=1.88J,动能的增加量
△Ek=1.81J(结果取3位有效数字).
④重锤在下落过程中的加速度a=9.50m/s2(结果取3位有效数字)
⑤出现实验误差的原因是重锤下落过程中受到阻力,大小Ff=0.3N.
分析 (1)解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项,只有理解了这些才能真正了解具体实验操作的含义.
(2)①重物下落时做匀加速运动,故纸带上的点应越来越远,根据这个关系判断那一端连接重物.
②验证机械能守恒时,我们验证的是减少的重力势能△Ep=mgh和增加的动能△Ek=$\frac{1}{2}$mv2之间的关系,所以我们要选择能够测h和v的数据.
③减少的重力势能△Ep=mgh,增加的动能△Ek=$\frac{1}{2}$mv2,v可由从纸带上计算出来.
④根据加速度公式a=$\frac{△x}{{T}^{2}}$,即可求解;
⑤依据牛顿第二定律,结合纸带加速度,即可求解.
解答 解:(1)B:将打点计时器应接到电源的“交流输出”上,故B错误.
C:因为我们是比较mgh、$\frac{1}{2}$mv2的大小关系,故m可约去比较,不需要用天平,故C错误.
(2):①重物下落时做匀加速运动,故纸带上的点应越来越远,故应该是左端连接重物.
②验证机械能守恒时,我们验证的是减少的重力势能△Ep=mgh和增加的动能△Ek=$\frac{1}{2}$mv2之间的关系,
所以我们要选择能够测h和v的数据.故选B点.
③减少的重力势能△Ep=mgh=1×9.8×19.2×10-2=1.88J
vB=$\frac{{x}_{AC}}{2T}$=$\frac{23.23-15.55}{2×0.02}×1{0}^{-2}$=1.92m/s
所以:增加的动能△Ek=$\frac{1}{2}$mv2=$\frac{1}{2}$×9.8×1.922=1.81J
④物体下落的加速度a=$\frac{△x}{{T}^{2}}$=$\frac{(23.23-19.20)-(19.20-15.55)}{0.0{2}^{2}}×1{0}^{-2}$=9.50m/s2,
⑤根据牛顿第二定律可以得到mg-f=ma,所以f=mg-ma=m(g-a)=1×(9.8-9.5)N=0.3N;
故答案为:(1)C,BD;(2)①左,②B,③1.88,1.81,④9.50m/s2,⑤0.3.
点评 纸带问题的处理时力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,注意有效数字的保留.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
| A. | 甲20s内的位移为150m | B. | 10s末甲乙相遇 | ||
| C. | 乙的加速度大小为1m/s2 | D. | 10s前甲在乙的前方 |
| A. | B=4T | B. | B≤4T | C. | B≥4T | D. | 无法确定 |
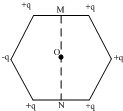 如图所示,六个点电荷分布在边长为a的正六边形的六个顶点处,除一处的电荷量为-q外,其余各处的电荷量均为+q,MN为其正六边形的一条中线,M、N为中线与正六边形边长相交的两点,则下列说法正确的是( )
如图所示,六个点电荷分布在边长为a的正六边形的六个顶点处,除一处的电荷量为-q外,其余各处的电荷量均为+q,MN为其正六边形的一条中线,M、N为中线与正六边形边长相交的两点,则下列说法正确的是( )| A. | M、N两点电势相等 | |
| B. | 沿直线从M到N移动负电荷,电势能一直增大 | |
| C. | M、N两点场强相同 | |
| D. | 在中心O处,场强大小为$\frac{2kq}{{a}^{2}}$,方向沿O指向-q方向 |
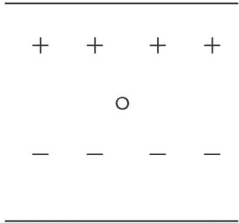
| A. | 该点磁感应强度大小一定是0.1 T | |
| B. | 该点磁感应强度大小一定不大于0.1 T | |
| C. | 该点磁感应强度大小一定不小于0.1 T | |
| D. | 该点磁感应强度的方向即为导线所受磁场力的方向 |

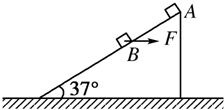 如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求:
如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求: