题目内容
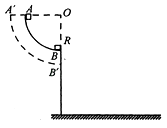
【题目】如图所示，两根长度相同的细线分别系有两个完全相同的小球，细线的上端系于O点；设法让两个小球均在水平面上做匀速圆周运动，已知L1跟竖直方向的夹角为60°，L2跟竖直方向的夹角为30°，下列说法正确的是（ ）
A.细线L1和细线L2所受的拉力大小之比为 1： 
B.小球m1和m2的角速度大小之比为 ：1
C.小球m1和m2的线速度大小之比为3 ：1
D.小球m1和m2的向心力大小之比为3：1
【答案】D
【解析】解：A、对任一小球研究．设细线与竖直方向的夹角为θ，竖直方向受力平衡，则：Tcosθ=mg，解得：T= 
，所以细线L1和细线L2所受的拉力大小之比 
= 
= 
，故A错误；
B、小球所受合力的大小为mgtanθ，根据牛顿第二定律得：mgtanθ=mLsinθω2，得：ω= 
．两小球Lcosθ相等，所以角速度相等，故B错误；
C、根据v=ωr，角速度相等，得小球m1和m2的线速度大小之比为： 
= 
= 
=3，故C错误；
D、小球所受合力提供向心力，则向心力为：F=mgtanθ，小球m1和m2的向心力大小之比为： 
= =3，故D正确．
故选：D．
小球受重力和拉力，两个力的合力提供小球做圆周运动的向心力．通过合力提供向心力，比较出两球的角速度大小，抓住小球距离顶点O的高度相同求出半径的关系，根据v=ωr比较线速度关系．
练习册系列答案
相关题目
