题目内容
【题目】如图所示，在一竖直平面内，y轴左方有一水平向右的场强为E1的匀强电场和垂直于纸面向里的磁感应强度为B1的匀强磁场，y轴右方有一竖直向上的场强为E2的匀强电场和另一磁感应强度为B2的匀强磁场.有一带电荷量为+q、质量为m的微粒，从x轴上的A点以初速度v与水平方向成θ角沿直线运动到y轴上的P点，A点到坐标原点O的距离为d.微粒进入y轴右侧后在竖直面内做匀速圆周运动，然后沿与P点运动速度相反的方向打到半径为r的1/4的绝缘光滑圆管内壁的M点(假设微粒与M点碰后速度改变、电荷量不变，圆管内径的大小可忽略，电场和磁场可不受影响地穿透圆管)，并恰好沿國管内无碰撞下滑至N点.己知θ=37°，sin37°=0.6，cos37°=0.8，求：
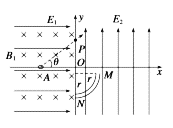
(1)E1与E2大小之比；
(2)y轴右侧的磁场的磁感应强度B2的大小和方向；
(3)从A点运动到N点所用的时间.
【答案】（1）
(2) 
，垂直纸面向外；（3）
【解析】(1)粒子A→P微粒做运动，受到电场力qE1，和重力mg及洛伦兹力qvB1，微粒做匀速直线运动，即三个力的合力为零，
根据几何关系得： qE1=mgtanθ
P→M微粒做匀速圆周运动，粒子受到电场力qE2，和重力mg及洛伦兹力qvB2，微粒做匀速圆周运动，则：qE2=mg
联立计算得出：E1：E2=3：4
(2)粒子沿与P点运动速度相反的方向打到半径为r的1/4的绝缘光滑圆管内壁的M点，则粒子恰好运动半个周期，
则由： 
，计算得出： 
洛伦兹力提供向心力： 
计算得出： 
又由左手定则可以知道B2的方向垂直纸面向外
(3)A→P做匀速直线运动有： 
计算得出
P→M有：vt2=πR
计算得出
碰到M点后速度只剩下向下的速度，此时qE2=mg，从M→N的过程中，微粒继续做匀速圆周运动
v1=vsin370
，计算得出
所以
