题目内容
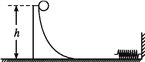
【题目】如图,第一次,小球从粗糙的![]() 圆形轨道顶端A由静止滑下,到达底端B的速度为v1,克服摩擦力做功为
圆形轨道顶端A由静止滑下,到达底端B的速度为v1,克服摩擦力做功为![]() W1;第二次,同一小球从底端B以v2冲上圆形轨道,恰好能到达A点,克服摩擦力做功为W2,C为
W1;第二次,同一小球从底端B以v2冲上圆形轨道,恰好能到达A点,克服摩擦力做功为W2,C为![]() 圆形轨道的中点,则下列说法正确的是
圆形轨道的中点,则下列说法正确的是

A. v1=v2
B. W1=W2
C. 小球第一次在B点对轨道的压力小于第二次在B点对轨道的压力
D. 小球第一次经过圆弧AC的过程中克服摩擦力做的功为![]() W1
W1
【答案】C
【解析】小球从A到B的过程,由动能定理得 mgh-W1=![]() mv12.小球从B到A的过程,由动能定理得-mgh-W2=0-
mv12.小球从B到A的过程,由动能定理得-mgh-W2=0-![]() mv22.即mgh+W2=
mv22.即mgh+W2=![]() mv22,对比可得 v1<v2.故A错误.同理可知,小球经过轨道上同一点时,上滑时的速度大于下滑时的速度,上滑时所需要的向心力大于下滑时所需要的向心力,而向心力是由轨道的支持力和重力垂直于轨道的分力的合力提供,所以上滑时所受的支持力大于下滑时所受的支持力,则同一点上滑时所受的摩擦力大于下滑时所受的摩擦力,而上滑与下滑两个过程路程相等,所以有W1<W2.故B错误.由上分析知,小球第一次在B点所受的支持力小于第二次在B点所受的支持力,由牛顿第三定律可知小球第一次在B点对轨道的压力小于第二次在B点对轨道的压力故C正确.从A到C的过程中小球所受的摩擦力的平均值小于从C到B的过程中摩擦力的平均值,所以从A到C的过程中克服摩擦力做功小于从C到B的过程中克服摩擦力做功,则小球第一次经过圆弧AC的过程中克服摩擦力做的功小于
mv22,对比可得 v1<v2.故A错误.同理可知,小球经过轨道上同一点时,上滑时的速度大于下滑时的速度,上滑时所需要的向心力大于下滑时所需要的向心力,而向心力是由轨道的支持力和重力垂直于轨道的分力的合力提供,所以上滑时所受的支持力大于下滑时所受的支持力,则同一点上滑时所受的摩擦力大于下滑时所受的摩擦力,而上滑与下滑两个过程路程相等,所以有W1<W2.故B错误.由上分析知,小球第一次在B点所受的支持力小于第二次在B点所受的支持力,由牛顿第三定律可知小球第一次在B点对轨道的压力小于第二次在B点对轨道的压力故C正确.从A到C的过程中小球所受的摩擦力的平均值小于从C到B的过程中摩擦力的平均值,所以从A到C的过程中克服摩擦力做功小于从C到B的过程中克服摩擦力做功,则小球第一次经过圆弧AC的过程中克服摩擦力做的功小于![]() W1.故D错误.故选C.
W1.故D错误.故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目