题目内容
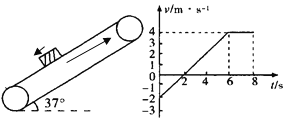
【题目】如图所示,倾角为37°足够长的传送带以4m/s的速度顺时针转动,现将小物块以2m/s的初速度沿斜面向下冲上传送带,小物块的速度随时间变化的关系如图所示,g=10m/s2,sin37°=0.6,cos37°=0.8,试求:
(1)小物块与传送带间的动摩擦因数为多大;
(2)0~8s内小物块与传送带之间的划痕为多长.
【答案】(1)![]() (2)18m
(2)18m
【解析】试题分析:根据v-t图象的斜率求出物体运动的加速度,由牛顿第二定律求解物体与传送带间的动摩擦因数;速度图象的“面积”大小等于位移,物体在0-2s内的位移为负值,在2-8s内的位移为正值;在前6s内物体与传送带发生相对滑动,求出相对位移△x。
(1)根据v-t图象的斜率表示加速度,可得物体的加速度大小为: ![]()
由牛顿第二定律得: ![]()
带入数据解得: ![]()
(2)0-8s内只有前6s内物体与传送带发生相对滑动
0-6s内传送带匀速运动距离为:s带=4×6m=24m 速度图象的“面积”大小等于位移,
则0-2s内物体位移为: ![]() ,方向沿斜面向下。
,方向沿斜面向下。
2-6s内物体位移为: ![]()
所以划痕的长度为: ![]()

练习册系列答案
相关题目