题目内容
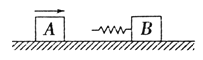
【题目】如图,两个滑块A和B的质量分别为4kg和2kg,放在静止于水平地面上的足够长的木板C上,两者与木板间的动摩擦因数均为0.4:木板的质量为2kg,与地面间的动摩擦因数为0.1.某时刻A滑块获得初速度v0=4m/s,0.5秒后A、B发生碰撞,碰撞过程时间极短AB总动能损失0.5J,设最大静摩擦力等于滑动摩擦力,不计滑块大小,取重力加速度大小g=10ms2.求
![]()
(1)求碰撞前滑块A和B的速度;
(2)A,B,C刚共速时候的速度。
【答案】(1)1.5m/s 2m/s(2)![]() m/s。
m/s。
【解析】
(1)碰撞前A滑块做匀减速运动,A受到的滑动摩擦力fA=μAmAg=0.4×4×10N=16N
根据牛顿第二定律得aA=-![]() =-μAg=-4m/s2
=-μAg=-4m/s2
碰撞前瞬间A的速度vA=v0+aAt=4-4×0.5=2m/s
碰撞前BC滑块看作一个整体做匀加速运动,则f地=μ地(mA+mB+mC)g
BC整体的加速度aBC=![]()
可得f地=8N,aBC=2m/s2
则vBC=aBCt=2×5=1m/s
(2)碰撞过程AB滑块动量守恒,取向右为正方向,则有:mAvA+mBvB=mAvA′+mBvB′
碰撞过程AB滑块能量守恒,有:![]() mAvA2+
mAvA2+![]() mBvB2=
mBvB2=![]() mAvA′2+
mAvA′2+![]() mBvB′2
mBvB′2
可以解得:vA′=1.5m/s,vB′=2m/s
或者vA′=![]() m/s,vB′=
m/s,vB′=![]() m/s。由于A滑块的速度不能大于B,所以舍去
m/s。由于A滑块的速度不能大于B,所以舍去
碰撞后A滑块受到摩擦力不变仍然为fA=16N
可得:aA=-4m/s2
碰撞后BC滑块B物体的速度大于C,不能看成一个整体。
B受到摩擦力fB=μBmBg
解得fB=8N
对C有aC=![]()
解得:aC=8m/s2
AC滑块相对运动直到共速过程
对A有vAC=vA′+aAt2。
对C有vAC=vBC+aCt2。
可得vAC=![]() m/s,t2=
m/s,t2=![]() s
s
然后B滑块继续减速(此过程AC共同恰好能匀速运动)直到ABC速度均为![]() m/s。
m/s。