Question

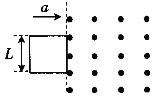
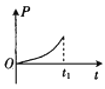
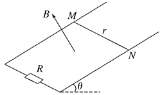
【题目】如图所示，足够长的U形导体框架的宽度L＝0.5 m，底端接有阻值R＝0.5 Ω的电阻，导体框架电阻忽略不计，其所在平面与水平面成θ＝37°角.有一磁感应强度B＝0.8 T的匀强磁场，方向垂直于导体框架平面向上.一根质量m＝0.4 kg、电阻r＝0.5 Ω的导体棒MN垂直跨放在U形导体框架上，某时刻起将导体棒MN由静止释放．已知导体棒MN与导体框架间的动摩擦因数μ＝0.5．（sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2）

（1）求导体棒刚开始下滑时的加速度大小；

（2）求导体棒运动过程中的最大速度大小；

（3）从导体棒开始下滑到速度刚达到最大的过程中，通过导体棒横截面的电荷量q＝4 C，求导体棒MN在此过程中消耗的电能．

Answer 1

【答案】（1）2 m/s2（2）5 m/s（3）1.5 J

【解析】

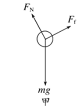
（1）导体棒刚开始下滑时，其受力情况如图甲所示，

则

mgsinθ－μmgcosθ＝ma

解得

a＝2 m/s2

（2）当导体棒匀速下滑时其受力情况如图乙所示，

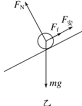
设匀速下滑的速度为v，则有

mgsin θ－Ff－F安＝0

摩擦力

Ff＝μmgcos θ

安培力

F安＝BIL＝

联立解得

（3）通过导体棒横截面的电荷量

设导体棒下滑速度刚好为最大速度v时的位移为x，则

ΔΦ＝BxL

由动能定理得，

mgx·sin θ－W安－μmgcos θ·x＝

其中W安为克服安培力做的功；

联立解得

W安＝3 J

克服安培力做的功等于回路在此过程中消耗的电能，即

Q＝3 J

则导体棒MN在此过程中消耗的电能

Qr＝Q＝1.5 J