题目内容
4.一小球以10米/秒的初速度,以60°的抛射角斜向上抛出,试求:(1)小球在最高点时的切向加速度和法向加速度?此时的轨道曲率半径是多少?
(2)小球下落到与抛出点同一水平面时,它的切向加速度与法向加速度是多少?此时轨道的曲率半径是多少?
分析 (1)对小球在最高点受力分析,求的法相加速度和切向加速度,根据$mg=\frac{m{v}^{2}}{R}$求的曲率半径
(2)根据物体做斜抛的对称性,求的落地点的速度,根据对加速度g的分解求的法相和切向加速度,根据$mg=\frac{m{v}^{2}}{R}$求的曲率半径
解答 解:(1)小球做斜抛运动,只在竖直方向受重力,故小球在最高点时的切向加速度为0,法向加速度为g,
在最高点的速度为v=v0cos60°=5m/s,根据$mg=\frac{m{v}^{2}}{R}$可得R=$\frac{{v}^{2}}{g}=\frac{{5}^{2}}{10}m=2.5m$
(2)根据做斜抛运动的对称性可知,落地时的速度与水平面的夹角为60°,速度为10m/s,根据加速度的分解可知法相加速度为:${a}_{n}=gsin30°=5m/{s}^{2}$
切向加速度$a′=gcos30°=5\sqrt{3}m/{s}^{2}$
根据$m{a}_{n}=\frac{m{v}^{2}}{R}$得R=$\frac{v{′}^{2}}{{a}_{n}}=\frac{1{0}^{2}}{5}m=20m$
答:(1)小球在最高点时的切向加速度和法向加速度分别为0和g,此时的轨道曲率半径是2.5m
(2)小球下落到与抛出点同一水平面时,它的切向加速度与法向加速度分别是$5\sqrt{3}m/{s}^{2}$和5m/s2,此时轨道的曲率半径是,20m
点评 本题主要考查了加速度的分解和速度的分解,会根据$mg=\frac{m{v}^{2}}{R}$求的曲率半径即可

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
19.点电荷Q、q分别放在A、B两点,下列说法正确的是( )
| A. | 当q的电量加倍时,Q在B点产生的电场强度的大小加倍 | |
| B. | 当q的电性改变时,Q在B点产生的电场强度的方向发生改变 | |
| C. | 当Q的电量加倍时,Q在B点产生的电场强度的大小加倍 | |
| D. | 当Q的电性改变时,Q在B点产生的电场强度的方向保持不变 |
20.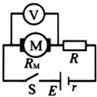 如图所示,一直流电动机与阻值R=9Ω的电阻串连接在电源上,电源电动势E=40V,内阻r=1Ω,用理想电压表测出电动机两端的电压U=20V,已知电动机线圈电阻RM=1Ω,则( )
如图所示,一直流电动机与阻值R=9Ω的电阻串连接在电源上,电源电动势E=40V,内阻r=1Ω,用理想电压表测出电动机两端的电压U=20V,已知电动机线圈电阻RM=1Ω,则( )
 如图所示,一直流电动机与阻值R=9Ω的电阻串连接在电源上,电源电动势E=40V,内阻r=1Ω,用理想电压表测出电动机两端的电压U=20V,已知电动机线圈电阻RM=1Ω,则( )
如图所示,一直流电动机与阻值R=9Ω的电阻串连接在电源上,电源电动势E=40V,内阻r=1Ω,用理想电压表测出电动机两端的电压U=20V,已知电动机线圈电阻RM=1Ω,则( )| A. | 通过电动机的电流为20A | B. | 电动机的输入功率为40W | ||
| C. | 电动机发热消耗的功率为10W | D. | 电动机输出的功率为30W |
9.一个质点沿半径为R的圆周运动一圈,回到原地,其路程与位移的大小分别为( )
| A. | 2πR,2R | B. | 2R,2πR | C. | 0,2R | D. | 2πR,0 |
13.某人站在20m的平台边缘,以10m/s的初速度竖直上抛一石子,则抛出后石子通过距抛出点5m处的时间可能是(不计空气阻力,取g=10m/s2)( )
| A. | 1s | B. | $\sqrt{2}$s | C. | 2s | D. | ($\sqrt{2}$+1)s |
14.如图所示,在同一轨道平面上同向旋的三个人造地球卫星A、B、C,在某一时刻恰好在同一条直线上,它们的轨道半径之比为1:2:3,则下列说法中正确的是( )


| A. | 三颗卫星的速度之比为1:4:9 | |
| B. | 三颗卫星的加速度之比为36:9:4 | |
| C. | B卫星加速后可与A卫星相遇 | |
| D. | A卫星运动27周后,C卫星也恰回到原地点 |
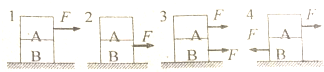
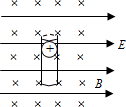 在绝缘的竖直放置的长塑料管内有一质量为0.1g,带电量q=4×10-4C的小球,管子处在如图所示的正交匀强电场和匀强磁场中,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里.已知B=0.5T,E=10V/m,小球与管壁间滑动摩擦系数μ=0.2.当小球从静止开始沿管子内壁下滑的过程中,加速度、速度最大各为多少?
在绝缘的竖直放置的长塑料管内有一质量为0.1g,带电量q=4×10-4C的小球,管子处在如图所示的正交匀强电场和匀强磁场中,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里.已知B=0.5T,E=10V/m,小球与管壁间滑动摩擦系数μ=0.2.当小球从静止开始沿管子内壁下滑的过程中,加速度、速度最大各为多少?