题目内容
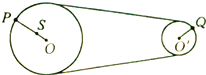
【题目】如图所示，压路机后轮半径是前轮半径的3倍，A、B分别为前轮和后轮边缘上的一点，C为后轮上的一点，它离后轮轴心的距离是后轮半径的一半，则A、B、C三点的角速度之比为ωA：ωB：ωC= ， 线速度之比为vA：vB：vC= ， 向心加速度之比为aA：aB：aC= ． 
【答案】3：1：1；2：2：1；6：2：1
【解析】A、B分别为同一传动装置前轮和后轮边缘上的一点，
所以有：VA=VB ，
因为rA：rB=1：3，所以ωA：ωB=3：1；
B、C两点共轴，所以有：ωC=ωB ．
所以：ωA：ωB：ωC=3：1：1；
线速度为：v=ωr ， 根据题意可知，AB共带，BC共轴，
所以有：vA：vB：vC=2：2：1
根据a=vω ， 可知，向心加速度之比为：aA：aB：aC=6：2：1；
所以答案是：3：1：1，2：2：1，6：2：1
练习册系列答案
相关题目
