题目内容
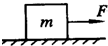如图所示，质量m=10kg的物体放在水平面上，物体与水平面间动摩擦因数为?=0.4，取 g=10m/s2．今用大小为F=50N的水平恒力作用于物体，使物体由静止开始作匀加速直线运动．经t=8s后撤去 F，求：（1）8s末物体的动能；
（2）物体从开始运动直到最终静止的整个过程中克服摩擦力所做的功．
分析：物体在粗糙水平面由静止被水平恒力拉着做匀加速直线运动，则由牛顿第二定律求出8s时的位移及速度．再由动能定理求出整个过程中克服摩擦力做的功．
解答：解：（1）物体受力分析，由合力求出加速度．则有：
F-μmg=ma
v=at
s=
at2
E=
mv2
由以上三式可得：E=320J s=32m
（2）选取物体从静止到停止过程，由动能定理可得：
则有：Fs-Wf克=0-0
解之得：Wf克=1600J．
答：（1）8s末物体的动能为320J；
（2）物体从开始运动直到最终静止的整个过程中克服摩擦力所做的功1600J．
F-μmg=ma
v=at
s=
| 1 |
| 2 |
E=
| 1 |
| 2 |
由以上三式可得：E=320J s=32m
（2）选取物体从静止到停止过程，由动能定理可得：
则有：Fs-Wf克=0-0
解之得：Wf克=1600J．
答：（1）8s末物体的动能为320J；
（2）物体从开始运动直到最终静止的整个过程中克服摩擦力所做的功1600J．
点评：8秒末物体的动能可以由动能公式求出，也可以由动能定理求出；而整个过程中克服摩擦力做的功，在运用动能定理时，过程选取从静止到停止，解题最简便．
练习册系列答案
相关题目
如图所示，质量M=1.0kg的木块随传送带一起以v=2.0m/s的速度向左匀速运动，木块与传送带间的动摩擦因数μ=0.50．当木块运动至最左端A点时，一颗质量m=20g的子弹以v0=3.0×102m/s水平向右的速度击穿木块，穿出木块时的速度v1=50m/s．设传送带的速度始终恒定，子弹击穿木块的时间极短，且不计木块质量变化，g=10m/s2．求：
如图所示，质量m=1.0kg的小球B静止在平台上，平台高h=0.8m．一个质量M=2.0kg的小球A沿平台自左向右运动，与小球B处发生正碰，碰后小球B的速度vB=6.0m/s，小球A落在水平地面的C点，DC间距离s=1.2m．求：
如图所示，质量m=1.0kg的物体静止水平面上，水平恒力F=3.0作用于物体上，使物体从静止开始运动，经时间t=2.0s撤去拉力F，已知物体与水平面间的动摩擦因数μ=0.15，取g=10m/s2．求：
如图所示，质量M=1.0kg，长L=l．0m的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ1=0.1kg．在木板的左端放置一个质量m=1.0kg、大小可以忽略的铁块，铁块与木板间的动摩擦因数μ2=0.4．认为最大静摩擦力等于滑动摩擦力，取g=10m/s2．若在铁块上加一个水平向右的恒力F=8.0N，求：