题目内容
11. 在如甲图所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B按如乙图所示的规律变化.则螺线管中产生的感应电动势E=1.2V;闭合S,电路中的电流稳定后,电阻R1的功率P1=5.76×10-2W;S断开后,流经R2的电量q=1.8×10-5C.
在如甲图所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B按如乙图所示的规律变化.则螺线管中产生的感应电动势E=1.2V;闭合S,电路中的电流稳定后,电阻R1的功率P1=5.76×10-2W;S断开后,流经R2的电量q=1.8×10-5C.
分析 根据法拉第地磁感应定律求出螺线管中产生的感应电动势.
根据楞次定律可知,感应电流的方向,从而确定电容器极板带电情况.
根据P=I2R求出电阻R1的电功率.
电容器与R2并联,两端电压等于R2两端的电压,根据Q=CU求出电容器的电量.
解答 解:由法拉第电磁感应定律可得,螺线管内产生的电动势为:
E=n$\frac{△B}{△t}$S=1500×$\frac{1-0.2}{2}$×20×10-4=1.2V;
电流稳定后,电流为:
I=$\frac{E}{{R}_{1}+{R}_{2}+r}$=$\frac{1.2}{4+5+1}$=0.12A,
电阻R1上消耗的功率为:
P=I2R1=0.122×4W=5.76×10-2 W;
电键断开后流经电阻R2的电荷量为:
Q=CU=CIR2=30×10-6×0.12×5C=1.8×10-5 C.
故答案为:1.2,5.76×10-2,1.8×10-5.
点评 本题是电磁感应与电路的综合,知道产生感应电动势的那部分相当于电源,运用闭合电路欧姆定律进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.一质点在X轴上运动(以向右为正方向),各个时刻的位置坐标如表:
则此质点从时刻t=0开始运动后:
(1)前2s内、前3s内、前5s内,质点通过的位移大小分是1、6、8,方向分别是向左、向左、向左.
(2)2s-3s内质点通过的位移是-5m,6s-7s内质点通过的位移是2m,位移较大的是哪段时间?2s-3s.
| t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x/cm | 3 | 5 | 2 | -3 | -2 | -5 | 1 | 3 | 5 |
(1)前2s内、前3s内、前5s内,质点通过的位移大小分是1、6、8,方向分别是向左、向左、向左.
(2)2s-3s内质点通过的位移是-5m,6s-7s内质点通过的位移是2m,位移较大的是哪段时间?2s-3s.
6. 如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
 如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )| A. | 副线圈交变电流的频率是100 Hz | B. | t=1s的时刻,电压表的示数为0 | ||
| C. | 变压器的输入电功率为220W | D. | 电流表的示数为$5\sqrt{2}$A |
3.做简谐运动的物体,每次经过同一位置时,不一定相同的物理量是( )
| A. | 加速度 | B. | 速度 | C. | 位移 | D. | 动能 |
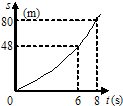 如图所示,为一物体的s-t图象,它是一抛物线,从图象中可以判定物体作匀加速直线运动,物体在8s内的位移是80m,物体运动48m所经历的时间是6s,物体在第7s末的瞬时速度大小是16m/s.
如图所示,为一物体的s-t图象,它是一抛物线,从图象中可以判定物体作匀加速直线运动,物体在8s内的位移是80m,物体运动48m所经历的时间是6s,物体在第7s末的瞬时速度大小是16m/s.
 如图所示,在xOy坐标平面的第一象限内有沿-y方向的匀强电场,在第四象限内有沿+y方向的匀强电场和垂直于平面向外的匀强磁场,且电场强度大小与第一象限相同.现有一质量为m,带电量为+q的质点,以某一初速度沿-x方向从坐标为(31,1)的P点开始运动,第一次经过x轴的点为Q点,Q点的坐标为(l,0),经过匀速圆周运动后第二次过x轴的点为坐标原点.若质点运动的初动能为2mgl,求:
如图所示,在xOy坐标平面的第一象限内有沿-y方向的匀强电场,在第四象限内有沿+y方向的匀强电场和垂直于平面向外的匀强磁场,且电场强度大小与第一象限相同.现有一质量为m,带电量为+q的质点,以某一初速度沿-x方向从坐标为(31,1)的P点开始运动,第一次经过x轴的点为Q点,Q点的坐标为(l,0),经过匀速圆周运动后第二次过x轴的点为坐标原点.若质点运动的初动能为2mgl,求: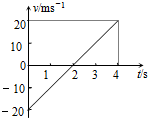 如图所示是某物体做匀变速直线运动的速度图线,某同学根据图线得出以下分析结论:
如图所示是某物体做匀变速直线运动的速度图线,某同学根据图线得出以下分析结论: