题目内容
17.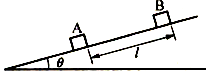 如图所示,足够长的斜面上,质量均为m的两物块A、B相距l,B与斜面间无摩擦,A与斜面间动摩擦因素为?(?>tanθ),B由静止开始下滑,与A发生弹性碰撞,碰撞时间极短可忽略不计,碰后A开始下滑,设在本题中最大静摩擦力等于滑动摩擦力,重力加速度为g.求:
如图所示,足够长的斜面上,质量均为m的两物块A、B相距l,B与斜面间无摩擦,A与斜面间动摩擦因素为?(?>tanθ),B由静止开始下滑,与A发生弹性碰撞,碰撞时间极短可忽略不计,碰后A开始下滑,设在本题中最大静摩擦力等于滑动摩擦力,重力加速度为g.求:(1)第一次碰撞结束瞬间物块A、B的速度各是多大?
(2)A,B再次相遇所需时间是多少?
分析 (1)B沿斜面向下匀加速运动,由动能定理求出B与A碰撞前的速度.B与A发生弹性碰撞,根据动量守恒定律和动能守恒列式,可求出第一次碰撞结束瞬间物块A、B的速度.
(2)A与B碰后,A做匀减速运动,B做匀加速运动.当两者位移相等时再次相遇,由牛顿第二定律和位移时间公式列式求解.
解答 解:(1)对B,匀加速下滑,令与A碰前速度为v1,则由动能定理得:
mglsinθ=$\frac{1}{2}m{v}_{1}^{2}$
解得 v1=$\sqrt{2glsinθ}$
对A、B的碰撞过程,令B与A碰后速度分别为v1′?和v2,取沿斜面向下方向为正方向,由动量守恒和能量守恒有:
mv1=mv1′+mv2.
$\frac{1}{2}$mv12=$\frac{1}{2}$mv1′2+$\frac{1}{2}$mv22.
解得 v1′=0,v2=$\sqrt{2glsinθ}$
(2)A与B碰后,A做匀减速运动,B做匀加速运动.
令B恰好在A停止时追上A所对应的摩擦因数为?0,则有
v2t-$\frac{1}{2}{a}_{2}{t}^{2}$=$\frac{1}{2}a{t}^{2}$
由牛顿第二定律得:
对B有 mgsinθ=ma
对A有 μ0mgcosθ-mgsinθ=ma2.
且 0=v2-a2t
得 μ0=2tanθ
如μ≤2tanθ,则B在A匀减速时追上A
对A有 μmgcosθ-mgsinθ=ma2.
由位移关系到 v2t-$\frac{1}{2}{a}_{2}{t}^{2}$=$\frac{1}{2}a{t}^{2}$
得 t=$\frac{2\sqrt{2glsinθ}}{μgcosθ}$
如?>2tanθ,则B在A停止后追上B
对A有,${v}_{2}^{2}$=2a2x
对B有,x=$\frac{1}{2}gsinθ{•t}^{2}$
解得 t=$\sqrt{\frac{2l}{g(μcosθ-sinθ)}}$
答:
(1)第一次碰撞结束瞬间物块A、B的速度各是$\sqrt{2glsinθ}$和0.
(2)若?≤2tanθ,A,B再次相遇所需时间是$\frac{2\sqrt{2glsinθ}}{μgcosθ}$;若?>2tanθ,A,B再次相遇所需时间是$\sqrt{\frac{2l}{g(μcosθ-sinθ)}}$.
点评 本题的关键是要分析清楚两个物体相遇的条件,注意临界条件分析与发散思维的运用,不能漏解.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
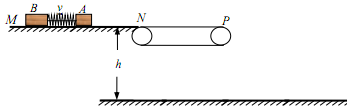
全优测试卷系列答案 测量运动员体能的装置如图所示,质量为m1的运动员将绳拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),下端悬吊一个m2的重物,人用力向后蹬传送带,而人的重心不动,使传送带以v的速率向后运动,则( )
测量运动员体能的装置如图所示,质量为m1的运动员将绳拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),下端悬吊一个m2的重物,人用力向后蹬传送带,而人的重心不动,使传送带以v的速率向后运动,则( )| A. | 人对传送带不做功 | B. | 传送带对人的冲量等于零 | ||
| C. | 人对传送带做功的功率m2gv | D. | 人对传送带做功的功率m1gv |
| A. | 一个原子核在一次衰变过程中可同时放出α、β、γ三种射线 | |
| B. | 结合能是核子结合成原子核而释放的能量 | |
| C. | 铀的裂变反应方程${\;}_{92}^{235}U+{\;}_0^1n→{\;}_{56}^{144}Ba+{\;}_{36}^{89}Kr+X{\;}_0^1n$中,X=3 | |
| D. | 若质子、电子具有相同的动能,则它们的物质波波长相等 |
| A. | 比结合能越小,表示原子核中核子结合得越牢固,原子核越稳定. | |
| B. | β衰变所释放的电子是原子核内的中子转化成质子时产生的 | |
| C. | 氢原子的核外电子,在由离核较远的轨道自发跃迁到离核较近的轨道的过程中,放出光子,电子动能减小,原子的电势能减小 | |
| D. | 某原子核经过一次α衰变和两次β衰变后,核内中子数减少6个 |
 如图所示是做匀变速直线运动的质点在0~6s内的位移-时间图线.若t=1s时,图线所对应的切线斜率为4(单位:m/s).则( )
如图所示是做匀变速直线运动的质点在0~6s内的位移-时间图线.若t=1s时,图线所对应的切线斜率为4(单位:m/s).则( )| A. | t=1s时,质点在x=5m的位置 | |
| B. | t=1s和t=5s时,质点的速度相同 | |
| C. | t=1s和t=5s时,质点加速度的方向相反 | |
| D. | 前5s内,合外力对质点做正功 |
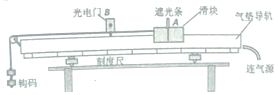 如图所示,是用光电计时器等器材做“验证机械能守恒定律”的实验,在滑块上安装一 遮光板,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电计时器安装在B处.测得滑块(含遮光板)质量为M、钩码总质量为m、遮光板宽度为d、当地的重力加速度为g.将滑块在图示A位置静止释放后,光电计时器记录下遮光板通过光电门的时间分别为△t.
如图所示,是用光电计时器等器材做“验证机械能守恒定律”的实验,在滑块上安装一 遮光板,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电计时器安装在B处.测得滑块(含遮光板)质量为M、钩码总质量为m、遮光板宽度为d、当地的重力加速度为g.将滑块在图示A位置静止释放后,光电计时器记录下遮光板通过光电门的时间分别为△t.