题目内容
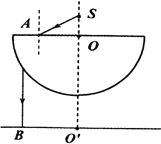
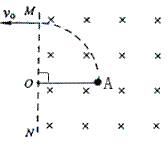
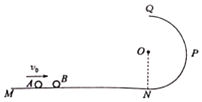
【题目】如图所示，MN为一水平光滑轨道，NPQ为光滑的竖直半圆轨道，NQ为半圆轨道的竖直直径，A、B为水平轨道上两小球，B小球静止在水平轨道上，A小球以某一初速度v与B小球发生正碰，
，已知碰后B小球恰好能通过半圆轨道的最高点
已知半四轨道的半径为r，物体A的质量为
，物体B的质量为
，重力加速度取g。求：
碰后小球B的速度
；
碰后小球A的速度
。
【答案】
=
=
【解析】
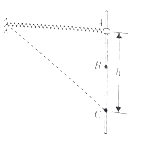
(1)
球恰好能通过Q点，重力提供向心力，由牛顿第二定律求出通过Q点的速度，应用机械能守恒定律求出碰撞后B的速度.
(2)两球碰撞过程动量守恒，应用动量守恒定律可以求出碰撞后A的速度.
(1)球恰好通过Q点，在Q点，由牛顿第二定律得：
，
从N到Q过程，对球B，由机械能守恒定律得：
，
解得：
；
(2)两球碰撞过程系统动量守恒，以向右为正方向，由动量守恒定律得：
，
解得：
；
练习册系列答案
相关题目
