Question

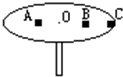
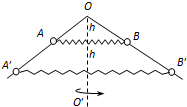
如图所示，由两根坚硬细杆所构成的三角形框架位于竖直平面内，∠AOB=120°，被铅垂线OO′平分．两个质量均为m的小环P、Q通过水平轻弹簧的作用恰好静止在A、B两处，相对细杆无滑动趋势．A、B连线与OO′垂直，连线与O点的距离为h，弹簧原长为

3

h，弹簧的形变始终在弹性限度内．环与杆间的动摩擦因数μ=

3

6

，且最大静摩擦力等于滑动摩擦力，重力加速度为g．试求：（1）弹簧的劲度系数k；
（2）现将两小环沿杆下移至A′B′处，使其在竖直方向上均下移h距离，同时释放两环．为使环在A′B′处不移动，可将整个框架绕OO′轴旋转，框架转动的角速度ω的范围是多少．

Answer 1

（1）环在A、B位置时，恰好处于平衡，根据共点力平衡得，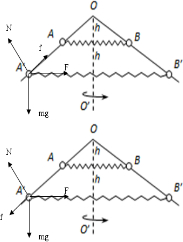
设弹簧的弹力为F，则有：Fcos30°=mgsin30°+μ（mgcos30°+Fsin30°）
解得F=

3 3 mg

5

，
弹簧的形变量x=2

3

h-

3

h=

3

h，
根据胡克定律得，F=kx，
解得k=

3mg

5h

．
（2）两小环沿杆下移至A′B′处，弹簧的形变量x′=4

3

h-

3

h=3

3

h，
弹簧的弹力F′=kx′=

9 3 mg

5

，
当最大静摩擦力沿杆向上时，根据牛顿第二定律得，水平方向上：F′+fcos30°-Nsin30°=m?2

3

hω12
竖直方向上有：fsin30°+Ncos30°=mg
f=μN
联立解得ω₁=

29g 35h

当最大静摩擦力沿杆向下时，根据牛顿第二定律得，水平方向上：F′-fcos30°-Nsin30°=m?2

3

hω22
竖直方向上有：fsin30°+mg=Ncos30°
f=μN，
联立解得ω₂=

3g 5h

．
所以角速度的范围为

3g 5h

≤ω≤

29g 35h

．
答：（1）弹簧的劲度系数为

3mg

5h

；
（2）框架转动的角速度ω的范围是

3g 5h

≤ω≤

29g 35h

．