题目内容
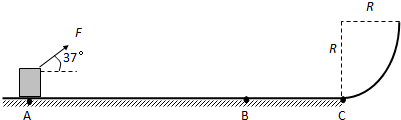
如图所示,粗糙水平面与半径R=2m的光滑
圆弧轨道相切于C点.静止于A处的物体,在大小为10N、方向与水平面成37°角的拉力F作用下沿水平面运动,到达C点时立即撤去F,物体沿光滑圆弧向上冲,然后返回经过C点进入水平面且停在B处.已知:物体返回经过C点时对轨道压力大小为物体重量的2.8倍,sAC=15m,sBC=4.5m,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)物体的质量
(2)物体与水平面的动摩擦因数.
| 1 |
| 4 |

(1)物体的质量
(2)物体与水平面的动摩擦因数.
返回C点时,根据牛顿第二定律得,N-mg=m
,N=2.8mg
解得vC=6m/s.
根据速度位移公式得,vC2=2asBC,解得a=
=
m/s2=4m/s2.
根据a=μg得,μ=0.4.
因为圆弧是光滑的,所以物体第一次到达C点的速度为6m/s.
根据速度位移公式得,匀加速运动的加速度大小a′=
=
m/s2=1.2m/s2.
根据牛顿第二定律得,a′=
代入数据解得m=2kg.
答:(1)物体的质量为2kg;
(2)物体与水平面的动摩擦因数为0.4.
| vC2 |
| R |
解得vC=6m/s.
根据速度位移公式得,vC2=2asBC,解得a=
| vC2 |
| 2sBC |
| 36 |
| 2×4.5 |
根据a=μg得,μ=0.4.
因为圆弧是光滑的,所以物体第一次到达C点的速度为6m/s.
根据速度位移公式得,匀加速运动的加速度大小a′=
| vC2 |
| 2sAC |
| 36 |
| 30 |
根据牛顿第二定律得,a′=
| Fcos37°-μ(mg-Fsin37°) |
| m |
代入数据解得m=2kg.
答:(1)物体的质量为2kg;
(2)物体与水平面的动摩擦因数为0.4.

练习册系列答案
相关题目