��Ŀ����
����Ŀ����ͼ����ʾ����xOy����ƽ��ԭ��O����һ����Դ������xOy����ƽ��2����120����Χ�ڸ���������ȷ�������Ϊm�������Ϊq�Ĵ��������ӣ����ӳ��ٶȴ�С��Ϊv0�������������������Ӽ�����á�
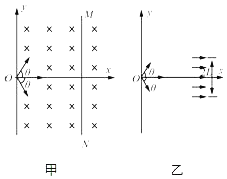
(1)��ͼ��y���Ҳ�Ӵ�ֱֽ�������ҷ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ��ΪB1����ֱ��x������㹻���ӫ����MN��
����x��ƽ��ӫ������ʹ���������Ӹպö����ܴ����ϣ����ʱӫ������O��ľ���d��
��������Դ�����������һ���ܴ�ӫ�����ϲ������գ������з���������ڴų����˶����ʱ�������ʱ��֮�ȣ�
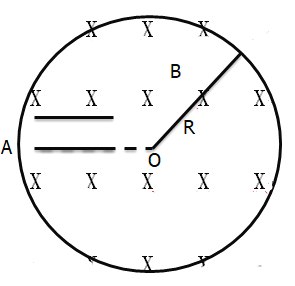
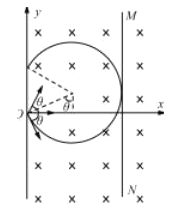
(2)��ʩ��������ֱֽ����н�Բ����ǿ�ų�����ʹ������Դ�������������Ӿ����ų�ƫת���Ϊһ������Ϊ2L����x���������ƽ������������ͼ����ʾ������ͼ���д��»����ų���������ų���������Ÿ�Ӧǿ�ȵĴ�СB2��
���𰸡���1����![]() ����
����![]() ����2��
����2��![]()
��������
��1�����������ڴų�����Բ���˶��뾶Ϊr1����![]()
��ͼ��ʾ���������Ӹպô�����Ӧ���㣺d��r1+r1sin��
��ã�![]() ��
��
����ͼ��֪��һ�������ܴ�ӫ�����ϣ��Ǵ�O������x���·������ӡ�����x���Ϸ����Ӵ�ӫ�����ϡ�
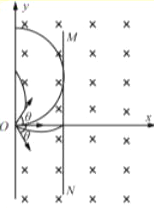
����Բ���˶������ڣ�![]()
�ʱ��![]()
���ʱ��![]()
��ã�![]() ��
��
��2����ͼ��ʾ���ų�����뾶RӦ����������Բ���˶��İ뾶r2��
�ɼ��ι�ϵ��r2��r2cos����L
��ţ�ٵڶ����ɣ�![]()
��ã�![]()


 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�