Question

【题目】如图所示,半径R=0.5m的绝缘圆形容器左侧有一平行板电容器,电容器内有电场,无磁场，两极板与水平直径平行,下极板刚好在水平半径OA上,下极板有一小孔C。一带正电的粒了从靠近上板处静止释放,经电场加速后从下小孔C处以竖直向下的速度出射,当粒子离开电场后就立即撤掉平行板电容器,同时加上垂直平面向里的匀强磁场B=10-2T。已知粒子的比荷为4108C/kg，C点与圆形容器最左端A距离为d,不计子的重力。求：

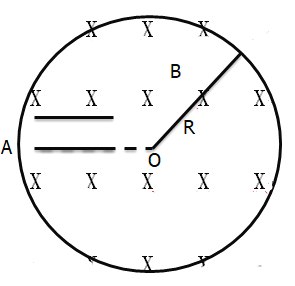
(1)当加速电压为U1=200V时,带电粒子在磁场中的运动半径；

(2)如果d=0.2m,为防止粒子打到绝缘容器上,加速电压U应满足什么条件；

(3)将磁场反向,调节加速电压,使粒子能垂直打到绝缘容器壁上,粒子与器壁碰撞后原速反弹且电量不变最后粒子好回到C点,则当d为多大时,粒子回到C点用时最短,最短时间为多少。

Answer 1

【答案】（1）0.1m（2）U1≤3200V（3）d=0.366m，

【解析】

（1）粒子先在电场中加速，后进入磁场做匀速圆周运动，由动能定理结合牛顿第二定律求解粒子的运动半径；（2）要使粒子打不到绝缘容器上的临界状态是粒子的轨迹恰好与容器相切，由几何关系求解半径，再求解加速电压的范围；（3）要使粒子再次回到C点且时间最短，则粒子与器壁碰撞3次，由几何关系求解半径，然后确定最短时间和D点的位置.

（1）粒子在加速电场中：U1q=mv02；

在磁场中做匀速圆周运动，则

联立解得

（2）如果d=0.2m，为防止粒子打到绝缘容器上，则

加速电压U应满足：

解得U1≤3200V

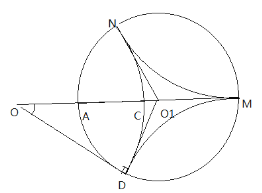
（3）要使粒子尽快回到C点，则粒子与器壁最少碰撞3次，如图；由几何关系可知， ，则粒子做圆周运动的半径 ，

则

最短时间为