Question

【题目】如图所示，半径为R的光滑绝缘半圆形轨道BPD位于竖直平面内，P为与圆心登高的点，D为最高点，其下端与水平绝缘轨道在B点平滑连接，水平轨道的BC段粗糙且BC=R，AC段光滑，竖直线BD的左侧轨道处在水平向右的匀强电场中，电场强度，现有一质量为m、带+q的小滑块（质点）. 第一次从A点由静止释放，在小滑块到达C点时即撤去电场，小滑块恰好能滑到P点；第二次从A点静止释放小滑块，在小滑块到达C点时保持电场强度大小不变方向变为竖直向上（半圆形轨道BPD也在该电场中），小滑块恰好能滑到D点，求：

（1）小滑块与BC段的动摩擦因数；

（2）AC段的长度L；

（3）小滑块从D点落在水平轨道上到B点的距离。

Answer 1

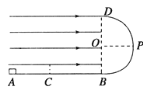
【答案】(1)μ＝0.5(2) L＝3R(3)x=2R

【解析】

(1)第一次小滑块恰好滑到P，从A到P由动能定理知

①

第二次从A到D由动能定理知

②

在D点有

③

联立以上①②③并代入得

μ＝0.5

(2)由①式代入E、μ得

L＝3R

(3)由上得

小滑块从D点落在水平轨道上到B点的过程做类平抛运动，加速度为

竖直方向有

水平方向有

联立解得

即小滑块从D点落在水平轨道上到B点的距离为2R。