题目内容
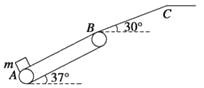
【题目】如图所示为某工厂的货物传送装置,倾斜运输带AB(与水平面成α=37°)与一斜面BC(与水平面成θ=30°)平滑连接,B点到C点的距离为L=0.6 m,运输带运行速度恒为v0=5 m/s,A点到B点的距离为x=4.5 m,现将一质量为m=0.4 kg的小物体轻轻放于A点,物体恰好能到达最高点C点,已知物体与斜面间的动摩擦因数μ1=![]() ,求:(g=10 m/s2,sin 37°=0.6,cos 37°=0.8,空气阻力不计)
,求:(g=10 m/s2,sin 37°=0.6,cos 37°=0.8,空气阻力不计)
(1) 小物体运动到B点时的速度v的大小;
(2) 小物体与运输带间的动摩擦因数μ;
(3) 小物体从A点运动到C点所经历的时间t.
【答案】(1)3 m/s.(2)7/8(3)3.4s
【解析】
(1)设小物体在斜面上的加速度为a1,运动到B点的速度为v,由牛顿第二定律得
mgsin θ+μ1mgcos θ=ma1
由运动学公式知v2=2a1L,联立解得v=3 m/s.
(2)因为v<v0,所以小物体在运输带上一直做匀加速运动,设加速度为a2,则由牛顿第二定律知
μmgcos α-mgsin α=ma2
又因为v2=2a2x,联立解得![]()
(3)小物体从A点运动到B点经历时间![]() ,从B运动到C经历时间
,从B运动到C经历时间![]()
联立并代入数据得小物体从A点运动到C点所经历的时间t=t1+t2=3.4 s.

练习册系列答案
相关题目