题目内容
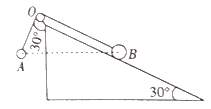
【题目】如图所示,长度为L的细绳上端固定在天花板上O点,下端拴着质量为m的小球.当把细绳拉直时,细绳与竖直线的夹角为θ=60°,此时小球静止于光滑的水平面上.
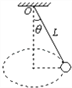
(1)当球以角速度ω1= ![]() 做圆锥摆运动时,水平面受到的压力N是多大?
做圆锥摆运动时,水平面受到的压力N是多大?
(2)当球以角速度ω2= ![]() 做圆锥摆运动时,细绳的张力T为多大?
做圆锥摆运动时,细绳的张力T为多大?
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1) 当球做圆锥摆运动时,在水平面内做匀速圆周运动,由重力、水平面的支持力和绳子拉力的合力提供向心力,根据牛顿第二定律,采用正交分解法列方程求解支持力;
(2) 当小球对桌面恰好无压力时,由重力和绳子拉力的合力提供向心力,根据牛顿第二定律求解此时小球的角速度,根据角速度![]() 与临界角速度的关系,判断小球是否离开桌面.若小球桌面做圆周运动,再由牛顿第二定律求解绳子的张力。
与临界角速度的关系,判断小球是否离开桌面.若小球桌面做圆周运动,再由牛顿第二定律求解绳子的张力。
解:(1)对小球受力分析,作出力图如图1.
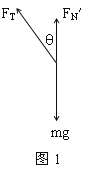
球在水平面内做匀速圆周运动,由重力、水平面的支持力和绳子拉力的合力提供向心力,则
根据牛顿第二定律,得
水平方向有:FTsin60°=mω12lsin60°①
竖直方向有:FN′+FTcos60°-mg=0②
又![]()
解得:![]() ;
;
(2) 设小球对桌面恰好无压力时角速度为ω0,即FN′=0
代入①②解得,![]()
由于![]() ,
,
故小球离开桌面做匀速圆周运动,则此时小球的受力如图2
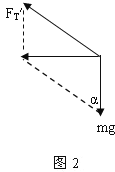
设绳子与竖直方向的夹角为α,则有
mgtanθ=mω22lsinα ③
mg=FT′cosα ④
联立解得 FT′=4mg。
点晴:本题是圆锥摆问题,分析受力,确定向心力来源是关键,要注意分析隐含的临界状态,运用牛顿运动定律求解。

练习册系列答案
相关题目