题目内容
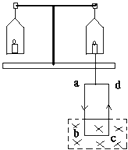
【题目】如图所示,内壁光滑长度为4l、横截面积为S的汽缸A、B,A水平、B竖直固定,之间由一段容积可忽略的细管相连,整个装置置于温度27℃、大气压为p0的环境中,活塞C、D的质量及厚度均忽略不计.原长3l、劲度系数 ![]() 的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点.开始活塞D距汽缸B的底部3l.后在D上放一质量为
的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点.开始活塞D距汽缸B的底部3l.后在D上放一质量为 ![]() 的物体.求:
的物体.求: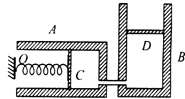
(1)稳定后活塞D下降的距离;
(2)改变汽缸内气体的温度使活塞D再回到初位置,则气体的温度应变为多少?
【答案】
(1)解:开始时被封闭气体的压强为 ![]() ,活塞C距气缸A的底部为l,被封气体的体积为4lS,重物放在活塞D上稳定后,被封气体的压强为:
,活塞C距气缸A的底部为l,被封气体的体积为4lS,重物放在活塞D上稳定后,被封气体的压强为:
![]()
活塞C将弹簧向左压缩了距离 ![]() ,则活塞C受力平衡,有:
,则活塞C受力平衡,有:
![]()
根据玻意耳定律,得: ![]()
解得:x=2l
![]()
活塞D下降的距离为: ![]()
答:稳定后活塞D下降的距离 ![]() ;
;
(2)解:升高温度过程中,气体做等压变化,活塞C的位置不动,最终被封气体的体积为 ![]() ,对最初和最终状态,根据理想气体状态方程得
,对最初和最终状态,根据理想气体状态方程得
![]()
解得: ![]()
答:改变汽缸内气体的温度使活塞D再回到初位置,则气体的温度应变为377℃
【解析】(1)开始时,活塞质量不计,容器内气体的压强等于大气压,弹簧处于原长;在活塞D上放上质量为m的物体后,活塞D下降后再次达到平衡时,由对活塞C受力平衡条件求得容器内气体的压强.封闭气体发生等温变化,根据玻意耳定律列式求解;(2)升高气缸内气体温度,当活塞D刚好回到初始位置,此过程中压强不变,弹簧的形变量不变,C的位置不变,对最初和最终根据理想气体状态方程列式即可求出气体温度

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目