题目内容
（12分）、如图所示，在一光滑水平的桌面上，放置一质量为M，宽为L的足够长“U”型框架，其ab部分电阻为R，框架其它部分的电阻不计。垂直框架两边放一质量为m、电阻为R的金属棒cd，它们之间的动摩擦因数为μ，棒通过细线跨过一定滑轮与劲度系数为 k 的另一端固定的轻弹簧相连。开始弹簧处于自然状态，框架和棒均静止。现在让框架在大小为2μmg的水平拉力作用下，向右做加速运动，引起棒的运动可看成是缓慢的。水平桌面位于竖直向上的匀强磁场中，磁感应强度为B。
问：（1）框架和棒刚开始运动的瞬间，框架的加速度为多大？
（2）框架最后做匀速运动（棒处于静止状态）时的速度多大？
（3）若框架通过位移S后开始匀速，已知弹簧的弹性势能的表达式为kx2/2（x为弹簧的形变量），则在框架通过位移S的过程中，回路中产生的电热为多少？
（1）
（2）
（3）
解析:（1）设水平拉力为F，则F＝2μmg，对框架由牛顿第二定律；
F一μmg＝Ma……………………………………………………………………（2分）
解出 ……………………………………………………………………（2分）
（2）设框架做匀速运动的速度大小为υ，则感应电动势
…………………………………………………………………………（1分）
回路中的电流
……………………………………………………（1分）
对框架由力的平衡得
……………………………………………（1分）
联立以上各式解出：………………………………………………（1分）
（3）在框架滑过S的过程中，设产生的电热为Ql ,摩擦生热为Q2，由功能关系
…………………………………………………（1分）
其中
……………………………………………………………（1分）
在框架匀速后，对棒由力的平衡得：
……………………………（1分）
联立以上各式并结合
解出………（1分）
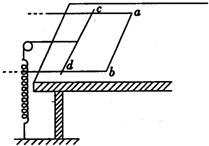（2013?河南模拟）如图所示，在一光滑水平的桌面上，放置一质量为M，宽为L的足够长“U”型框架，其ab部分电阻为R，框架其它部分的电阻不计．垂直框架两边放一质量为m、电阻为R的金属棒cd，它们之间的动摩擦因数为μ，棒通过细线跨过一定滑轮与劲度系数为k的另一端固定的轻弹簧相连．开始弹簧处于自然状态，框架和棒均静止．现在让框架在大小为2μmg的水平拉力作用下，向右做加速运动，引起棒的运动可看成是缓慢的．水平桌面位于竖直向上的匀强磁场中，磁感应强度为B．问：
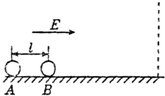如图所示，在一光滑绝缘水平面上，静放着两个可视为质点的小球，两小球质量均为m，相距l，其中A带正电，所带电荷量为q，小球B不带电．若加一水平向右的匀强电场，场强为E，A球受到电场力的作用向右运动与B球碰撞．设每次碰撞前后两球交换速度，且碰撞过程无电荷转移．若两小球恰在第三次碰撞时离开电场，求：
如图所示，在一光滑的水平面上有两块相同的木板B和C．重物A（视为质点）位于B的右端，A、B、C的质量相等．现A和B以同一速度滑向静止的C，B与C发生正碰．碰后B和C粘在一起运动，A在C上滑行，A与C有摩擦力．已知A滑到C的右端而未掉下．试问：从B、C发生正碰到A刚移动到C右端期间，C所走过的距离是C板长度的多少倍？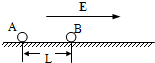
如图所示，在一光滑绝缘的水平面上，静置两个质量均为m，相距为L的小球，其中A球带正电q，B球不带电．若在水平面上加一水平向右的匀强电场，场强为E．A球受电场力作用，向右运动与B球碰撞，设每次碰撞前后两球交换速度，并且碰撞过程无电荷转移．问：在A、B两球第n次碰撞前瞬间，A球通过的总位移S．