题目内容
如图所示,xoy平面内存在着沿y轴正方向的匀强电场,一个质量为m、电荷量为+q的粒子从坐标原点O以速度v0沿x轴正方向开始运动。当它经过图中虚线上的 点时,撤去电场,粒子继续运动一段时间进入一个矩形匀强磁场区域(图中未画出),后又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点,已知磁场方向垂直xOy平面向里,磁感应强度大小为B,不计粒子的重力。求:
点时,撤去电场,粒子继续运动一段时间进入一个矩形匀强磁场区域(图中未画出),后又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点,已知磁场方向垂直xOy平面向里,磁感应强度大小为B,不计粒子的重力。求:
(1)电场强度的大小;
(2)N点的坐标;
(3)矩形磁场的最小横截面积。
 点时,撤去电场,粒子继续运动一段时间进入一个矩形匀强磁场区域(图中未画出),后又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点,已知磁场方向垂直xOy平面向里,磁感应强度大小为B,不计粒子的重力。求:
点时,撤去电场,粒子继续运动一段时间进入一个矩形匀强磁场区域(图中未画出),后又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点,已知磁场方向垂直xOy平面向里,磁感应强度大小为B,不计粒子的重力。求:
(1)电场强度的大小;
(2)N点的坐标;
(3)矩形磁场的最小横截面积。
(1)E= (2)(
(2)( (3)
(3)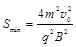
 (2)(
(2)( (3)
(3)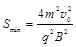
试题分析:如图是粒子的运动过程示意图。

(1) 粒子从O到M有
 ① 1分
① 1分  ② 1分
② 1分qE=ma ③ 1分
解得E=
 ④ 1分
④ 1分 (2) 设粒子运动到M点时速度为v,
与x轴正方向的夹角为α,则
 ⑤ 1分
⑤ 1分 ⑥ 1分
⑥ 1分tan
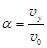 ⑦ 1分
⑦ 1分粒子在磁场中从P到N
qvB=
 ⑧ 1分
⑧ 1分由几何关系知,
 30°
30°在N点有
 ⑨ 1分
⑨ 1分
故N点的坐标为(
 ) ⑩ 1分
) ⑩ 1分(3) 矩形磁场的两个边长分别为
 ? 1分
? 1分 ? 2分
? 2分矩形磁场的最小面积
 ? 1分
? 1分解得
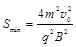 ? 2分
? 2分点评:有该题看出,分清物理过程,不同物理过程应用相应的物理知识;抓住关键字句,分析出关键条件.如该题中粒子从N点沿MN的方向射出,即可分析出速度方向,再利用相关知识来“定圆心,找半径”;此外良好的作图能力及几何分析能力是解决此类问题的关键

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 向
向 运动,运动的轨迹如图中的虚线所示,若
运动,运动的轨迹如图中的虚线所示,若 ,
, ,则
,则

 ,负
,负 ,负
,负

 ,质量为m,(重力不计)求:
,质量为m,(重力不计)求:


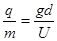 的带正电质点以相同的初速沿A、B板的中心线相继射入,如图所示.第一个质点射入后恰好落在B板的中点处.接着,第二个质点射入极板间,运动一段时间
的带正电质点以相同的初速沿A、B板的中心线相继射入,如图所示.第一个质点射入后恰好落在B板的中点处.接着,第二个质点射入极板间,运动一段时间 后, A板电势突然变为
后, A板电势突然变为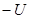 并且不再改变,结果第二个质点恰好没有碰到极板.求:
并且不再改变,结果第二个质点恰好没有碰到极板.求:
 .
.