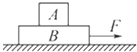
题目内容
【题目】如图所示，将带电量
＝
、质量
＝
的滑块放在小车的绝缘板的右端，小车的质量
＝
，滑块与绝缘板间动摩擦因数
＝
，小车的绝缘板足够长，它们所在的空间存在着磁感应强度
＝
的水平方向的匀强磁场．开始时小车静止在光滑水平面上，一摆长
＝
、摆球质量
＝
的摆从水平位置由静止释放，摆到最低点时与小车相撞，如图所示，碰撞后摆球恰好静止，
＝
，求：
（1）与车碰撞前摆球到达最低点时对绳子的拉力；
（2）球与小车的碰撞过程中系统损失的机械能
；
（3）碰撞后小车的最终速度．
【答案】（1）
；（2）
（3）
，方向水平向右
【解析】
(1) 小球向下摆动过程，只有重力做功，其机械能守恒，由机械能守恒定律得：
解得：
在最低点，由牛顿第二定律得：
代入数据解得：
F=4.5N
(2) 摆球与小车碰撞过程中的过程中，两者组成的系统动量守恒定律，以摆球的初速度方向为正方向，由动量守恒定律得：
mv=Mv1+0
代入数据解得：
v1=1.5m/s
摆球与小车碰撞过程中系统损失的机械能为：
代入数据解得：
△E=1.31J
(3) 假设m′最终能与M一起运动，由动量守恒定律得：
Mv1=（M+m′）v2
代入数据解得：
v2=0.9375m/s
m′受到的向上洛仑兹力为：
f=BQv2=20×0.3×0.9375=5.625N＞m′g=1.5N
所以m′在还未到v2=3m/s时已与M分开了，对物块：
Qv3B=m′g
代入数据解得：
v3=0.5m/s
物块与车组成的系统动量守恒，以物块的初速度方向为正方向，由动量守恒定律可得：
Mv1=Mv2′+m′v3
代入数据解得：
v2′=1.2m/s
方向水平向右．
练习册系列答案
相关题目
