题目内容
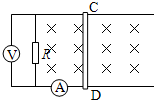 如图所示,电阻r=0.3Ω、质量m=0.1kg的金属CD垂直跨搁在位于水平面上的两条平行光滑金属轨道上,两导轨间距为L,棒与导轨间接触良好,导轨左端接有R=0.5Ω的电阻,量程为0~3.0A的电流表串接在一条轨道上,量程为0~1.0V的电压表接在电阻R两端,垂直导轨平面的匀强磁场向下穿过平面,现以向右恒定外力F使金属棒右移,当金属棒以v=2m/s的速度在居轨平面上匀速滑动时,观察到电路中一个电表正好满偏,而另一个电表未满偏.求:
如图所示,电阻r=0.3Ω、质量m=0.1kg的金属CD垂直跨搁在位于水平面上的两条平行光滑金属轨道上,两导轨间距为L,棒与导轨间接触良好,导轨左端接有R=0.5Ω的电阻,量程为0~3.0A的电流表串接在一条轨道上,量程为0~1.0V的电压表接在电阻R两端,垂直导轨平面的匀强磁场向下穿过平面,现以向右恒定外力F使金属棒右移,当金属棒以v=2m/s的速度在居轨平面上匀速滑动时,观察到电路中一个电表正好满偏,而另一个电表未满偏.求:(1)拉动金属棒的外力F多大?
(2)此时撤去外力F,金属棒将逐渐慢下来,最终停止在导轨上,求从撤去外力到金属棒停止运动的过程中通过电阻R的电量.
分析:(1)采用假设法分析哪只电表满偏.假设电压表满偏,由欧姆定律求出通过电流表的电流,与电流表的量程比较,确定是否合理.金属棒做匀速运动,水平拉力F与金属棒所受的安培力大小相等、方向相反.由F=BId求出安培力,即可得解.
(2)若某时刻撤去外力,从撤去外力到金属棒停止运动,由牛顿第二定律可列出表达式,在时间的积累上求和,从而算出滑行的位移,再由电量q=
即可求解.
(2)若某时刻撤去外力,从撤去外力到金属棒停止运动,由牛顿第二定律可列出表达式,在时间的积累上求和,从而算出滑行的位移,再由电量q=
| △? |
| R+r |
解答:解:(1)假设电压表满偏,则通过变阻器的电流为I=
=
A=2A,而电流表量程为0~3.0A,所以电压表满偏正常,电流表的示数为2A.
若电流表满偏,则通过变阻器的电压为UIR=3×0.5V=1.5V,此时电压已超出电压表的最大量程,故只能让电压表满偏.
棒匀速运动时,水平拉力F与安培力大小相等,则有F=FA=BIL,
解得 F=1.6 N.
(2)由上问可知,BL=
=
N=0.8N,
根据牛顿第二定律可得,
=ma,
对上式两边在时间的积累,则有
=mv,
从而求出滑行的位移为:x=
产生的感应电动势E=
,
而欧姆定律I=
电量,q=I?△t
则有:通过电阻的电量q=
=
=0.25C
答:(1)1.6N,(2)0.25C
| U |
| R |
| 1 |
| 0.5 |
若电流表满偏,则通过变阻器的电压为UIR=3×0.5V=1.5V,此时电压已超出电压表的最大量程,故只能让电压表满偏.
棒匀速运动时,水平拉力F与安培力大小相等,则有F=FA=BIL,
解得 F=1.6 N.
(2)由上问可知,BL=
| F |
| I |
| 1.6 |
| 2 |
根据牛顿第二定律可得,
| B2L2v |
| R+r |
对上式两边在时间的积累,则有
| B2L2x |
| R+r |
从而求出滑行的位移为:x=
| mv(R+r) |
| B2L2 |
产生的感应电动势E=
| △? |
| △t |
而欧姆定律I=
| E |
| R+r |
电量,q=I?△t
则有:通过电阻的电量q=
| △? |
| R+r |
| B?L×x |
| R+r |
答:(1)1.6N,(2)0.25C
点评:本题是电磁感应与电路知识的综合应用,要抓住电动势既与电路有联系,又与电磁感应有联系.根据法拉第电磁感应定律与闭合电路欧姆定律及电量表达式,则可求出通过电阻的电量q=
.
| △? |
| R+r |

练习册系列答案
相关题目
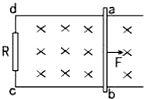 如图所示,电阻r=0.1Ω的导体棒ab沿光滑的导线框向右做匀速运动,线框左端接有电阻R=0.4Ω,线框放在磁感应强度B=0.1T的匀强磁场中,磁场方向垂直于线框所在平面,导体棒ab的长度L=0.4m,运动速度v=5.0m/s.线框的电阻不计.
如图所示,电阻r=0.1Ω的导体棒ab沿光滑的导线框向右做匀速运动,线框左端接有电阻R=0.4Ω,线框放在磁感应强度B=0.1T的匀强磁场中,磁场方向垂直于线框所在平面,导体棒ab的长度L=0.4m,运动速度v=5.0m/s.线框的电阻不计.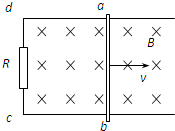 如图所示,电阻r=0.1Ω的导体棒ab沿光滑导体框向右做匀速运动,线框接有电阻R=0.4Ω.线框放在磁感强度B=0.1T的匀强磁场中,磁场方向垂直线框平面.导体棒ab的长度L=0.2m,运动速度v=5m/s,线框电阻不计.试求:
如图所示,电阻r=0.1Ω的导体棒ab沿光滑导体框向右做匀速运动,线框接有电阻R=0.4Ω.线框放在磁感强度B=0.1T的匀强磁场中,磁场方向垂直线框平面.导体棒ab的长度L=0.2m,运动速度v=5m/s,线框电阻不计.试求: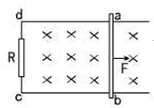 如图所示,电阻R=0.1Ω的导体ab沿光滑的导线框向右做匀速运动,线框中接有电阻R=0.4Ω线框放在磁感应强度B=0.1T的匀强磁场中,磁场方向垂直于线框平面,导体ab的长度L=0.4m,运动速度v=5.0m/s.线框的电阻不计.
如图所示,电阻R=0.1Ω的导体ab沿光滑的导线框向右做匀速运动,线框中接有电阻R=0.4Ω线框放在磁感应强度B=0.1T的匀强磁场中,磁场方向垂直于线框平面,导体ab的长度L=0.4m,运动速度v=5.0m/s.线框的电阻不计.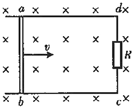 如图所示,电阻r=0.5Ω的导体棒ab沿光滑的水平导线框向右做匀速运动,线框宽L=0.5m,处于竖直向下的匀强磁场中,磁感应强度B=1.0T,线框接有电阻R=2.5Ω,线框电阻不计,当ab棒的运动速度v=3.0m/s时,ab棒产生的感应电动势为
如图所示,电阻r=0.5Ω的导体棒ab沿光滑的水平导线框向右做匀速运动,线框宽L=0.5m,处于竖直向下的匀强磁场中,磁感应强度B=1.0T,线框接有电阻R=2.5Ω,线框电阻不计,当ab棒的运动速度v=3.0m/s时,ab棒产生的感应电动势为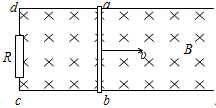 固定于水平绝缘平面上的光滑平行金属导轨,间距L=0.4m,c、d间接一阻值为R=0.4Ω的定值电阻,垂直于导轨平面有磁感应强度B=0.1T的匀强磁场,俯视图如图所示,电阻r=0.1Ω、长为0.4m的金属棒ab与导轨接触良好,现金属棒ab在水平外力作用下以v=5m/s的速度沿导轨向右匀速运动,其余电阻不计,求:
固定于水平绝缘平面上的光滑平行金属导轨,间距L=0.4m,c、d间接一阻值为R=0.4Ω的定值电阻,垂直于导轨平面有磁感应强度B=0.1T的匀强磁场,俯视图如图所示,电阻r=0.1Ω、长为0.4m的金属棒ab与导轨接触良好,现金属棒ab在水平外力作用下以v=5m/s的速度沿导轨向右匀速运动,其余电阻不计,求: