题目内容
 用一根长为l的轻质不可伸长的细绳把一个质量为m的小球悬挂在点O,将小球拉至与悬点等高处由静止释放,如图所示.求:
用一根长为l的轻质不可伸长的细绳把一个质量为m的小球悬挂在点O,将小球拉至与悬点等高处由静止释放,如图所示.求:(1)小球经过最低点时的速度大小;
(2)小球经过最低点时,细绳的拉力F.
分析:(1)小球向下运动的过程中,绳子拉力不做功,只有重力做功,满足机械能守恒的条件,即可根据机械能守恒定律列式求解;
(2)小球经过最低点时,由细绳的拉力F和重力的合力提供向心力,根据牛顿第二定律求F.
(2)小球经过最低点时,由细绳的拉力F和重力的合力提供向心力,根据牛顿第二定律求F.
解答:解:(1)从静止运动到最低点的过得中,机械能守恒,则有
mgl=
mv2
则得:小球经过最低点时的速度大小为v=
(2)在最低点,根据牛顿第二定律得:
F-mg=m
联立上两式得:F=3mg
答:
(1)小球经过最低点时的速度大小是
.
(2)小球经过最低点时,细绳的拉力F为3mg.
mgl=
| 1 |
| 2 |
则得:小球经过最低点时的速度大小为v=
| 2gl |
(2)在最低点,根据牛顿第二定律得:
F-mg=m
| v2 |
| l |
联立上两式得:F=3mg
答:
(1)小球经过最低点时的速度大小是
| 2gl |
(2)小球经过最低点时,细绳的拉力F为3mg.
点评:本题是机械能守恒与向心力知识的综合,对于本题的结论要理解记忆,其中F的大小与绳长无关的特点要特别关注.

练习册系列答案
相关题目
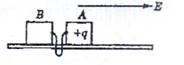
 如图所示,在光滑水平长直轨道上有A、B两个绝缘体,它们之间有一根长为l的轻质软线相连接,其中A的质量为m,B的质量为M=4m,A为带有电荷量为q的正电荷,B不带电,空间存在着方向水平向右的匀强电场,场强大小为E.开始时用外力把A与B靠在一起并保持静止,某时刻撤去外力,A开始向右运动,直到细线绷紧.当细线被绷紧时,两物体将有极短时间的相互作用,而后B开始运动,且细线再次松弛.已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的
如图所示,在光滑水平长直轨道上有A、B两个绝缘体,它们之间有一根长为l的轻质软线相连接,其中A的质量为m,B的质量为M=4m,A为带有电荷量为q的正电荷,B不带电,空间存在着方向水平向右的匀强电场,场强大小为E.开始时用外力把A与B靠在一起并保持静止,某时刻撤去外力,A开始向右运动,直到细线绷紧.当细线被绷紧时,两物体将有极短时间的相互作用,而后B开始运动,且细线再次松弛.已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的 如图所示,一根长为l的轻质直杆,可绕光滑转轴O自由转动,在其中点、上端分别固定质量均为m的小球B、A,小球A用水平绳系住,使杆与水平面成53°角.
如图所示,一根长为l的轻质直杆,可绕光滑转轴O自由转动,在其中点、上端分别固定质量均为m的小球B、A,小球A用水平绳系住,使杆与水平面成53°角.