题目内容
(2010?永州一模)如图所示,在光滑的绝缘水平面上,有导体A和绝缘体B两个物体,它们之间用一根长为L的轻质绝缘细线相连,其中A的质量为m,带电量为q,B的质量为4m,不带电.开始时A和B靠近在一起并保持静止.某一时刻施加一个水平向右、大小为E的匀强电场,A开始向右运动,当细线绷紧时其张力远大于A所受到的电场力,在极短时间内B获得一个速度,其大小等于细线绷紧前瞬间A的速度的三分之一.求:

(1)细线第一次绷紧前瞬间A的速度大小;
(2)若细线在第二次绷紧前A、B没有发生碰撞,求物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量.

(1)细线第一次绷紧前瞬间A的速度大小;
(2)若细线在第二次绷紧前A、B没有发生碰撞,求物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量.
分析:(1)在细线拉紧前,A做匀加速运动,由动能定理可以求出A获得的速度;
(2)细线拉紧的瞬间,A、B组成的系统动量守恒,由动量守恒定律可以求出A的速度;碰后A先向左做减速运动,后向右做初速度为零的匀加速运动,B做匀速直线运动,如果A与B位移再次相差l时,细线第二次绷紧.由运动学公式分析答题.
(2)细线拉紧的瞬间,A、B组成的系统动量守恒,由动量守恒定律可以求出A的速度;碰后A先向左做减速运动,后向右做初速度为零的匀加速运动,B做匀速直线运动,如果A与B位移再次相差l时,细线第二次绷紧.由运动学公式分析答题.
解答:解:(1)由动能定理得qEl=
m
解得:v0=
(2)设细线第一次绷紧后的瞬间A的速度为v1,B的速度为v2,
因细线绷紧过程所用时间极短,电场力的冲量qE△t极小,可以忽略不计,根据动量守恒定律有
mvo=mv1+4mv2,v2=
v0
解得:v1=-
第一次绷紧后A的速度为
,负号表示速度的方向水平向左.
设第一次绷紧后到第二次绷紧经历的时间t,则:
A的位移:SA=v1t+
at2
a=
B的位移:SB=v2t
再次相碰时:SA-SB=l
第1次绷紧前A的位移:2al=
-0
联立以上各式,解得:SA=
l
物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量等于电场力对A做功:△E=W=qE(l+SA)=
qEl.
答:(1)(1)细线第一次绷紧前瞬间A的速度大小为
;
(2)物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量为△E=
qEl.
| 1 |
| 2 |
| v | 2 0 |
解得:v0=
|
(2)设细线第一次绷紧后的瞬间A的速度为v1,B的速度为v2,
因细线绷紧过程所用时间极短,电场力的冲量qE△t极小,可以忽略不计,根据动量守恒定律有
mvo=mv1+4mv2,v2=
| 1 |
| 3 |
解得:v1=-
| v0 |
| 3 |
第一次绷紧后A的速度为
| v0 |
| 3 |
设第一次绷紧后到第二次绷紧经历的时间t,则:
A的位移:SA=v1t+
| 1 |
| 2 |
a=
| qE |
| m |
B的位移:SB=v2t
再次相碰时:SA-SB=l
第1次绷紧前A的位移:2al=
| v | 2 0 |
联立以上各式,解得:SA=
13+2
| ||
| 9 |
物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量等于电场力对A做功:△E=W=qE(l+SA)=
22+2
| ||
| 9 |
答:(1)(1)细线第一次绷紧前瞬间A的速度大小为
|
(2)物体A从开始运动到细线第二次绷紧过程中A的电势能的改变量为△E=
22+2
| ||
| 9 |
点评:分析清楚物体的运动过程越运动性质,应用动能定理、动量守恒定律、运动学公式即可正确解题.

练习册系列答案
相关题目
 (2010?永州一模)如图所示,在水平的光滑平板上的O点固定一根原长为l0的劲度系数为k的轻弹簧,在弹簧的自由端连接一个质量为m的小球(可视为质点).若弹簧始终处在弹性范围内,今将平板以O为转轴在竖直平面内逆时针缓慢转动,直至平板变为竖直状态,则在此过程中( )
(2010?永州一模)如图所示,在水平的光滑平板上的O点固定一根原长为l0的劲度系数为k的轻弹簧,在弹簧的自由端连接一个质量为m的小球(可视为质点).若弹簧始终处在弹性范围内,今将平板以O为转轴在竖直平面内逆时针缓慢转动,直至平板变为竖直状态,则在此过程中( )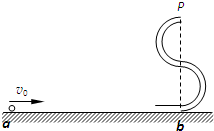 (2010?永州一模)“S”形玩具轨道如图所示.该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内.轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个直径略小于细管直径的小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从P点水平抛出.已知小球与地面ab段间的动摩擦因数μ=0.2,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若v0=
(2010?永州一模)“S”形玩具轨道如图所示.该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内.轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个直径略小于细管直径的小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从P点水平抛出.已知小球与地面ab段间的动摩擦因数μ=0.2,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若v0=