题目内容
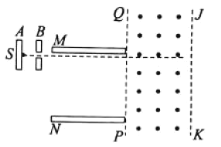
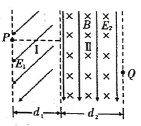
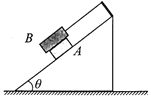
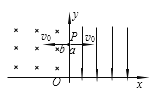
【题目】如图所示,在直角坐标系xOy的第一象限的空间内存在沿y轴负方向、电场强度E=200V/m的匀强电场,第二象限的空间内存在垂直纸面向里、磁感应强度B=0.125T的匀强磁场。质量均为m=4.0×10-15kg、电荷量均为q=+2.0×10-9C的两带电粒子a、b先后以v0=5.0×103m/s的速率,从y轴上P点沿x轴正、负方向射出,PO之间的距离h=8.0×10-2m,经过一段时间后,两粒子先后通过x轴。若两粒子之间的相互作用、所受重力以及空气阻力均可忽略不计,求:
(1)粒子a在电场中运动的时间t1;
(2)粒子b在磁场中运动的半径Rb;
(3)a、b两粒子通过x轴时,它们的动能之比;
(4)粒子b从P点到通过x轴所用时间t2;
(5)a、b两粒子通过x轴时,它们的速度方向之间的夹角θ。
【答案】(1)4.0×10-5s;(2)0.08m;(3)41:25;(4)2.5×10-5s;(5)![]()
【解析】
(1) 粒子a在电场中做类平抛运动,在竖直方向上
![]()
![]()
供入数据,整理得
![]()
(2)根据牛顿第二定律
![]()
代入数据,得
![]()
(3) 粒子a到达x轴时
![]()
因此
![]()
而粒子b在磁场中做匀速圆周运动,到达x轴时的速度大小仍为![]() ,因此
,因此
![]()
(4)由于
![]()
根据几何关系可知,圆心恰好在坐标原点,粒子b从P点到通过x轴恰好运动了![]() 个圆周,所用时间
个圆周,所用时间
![]()
(5)由于能通过x轴后粒子b恰好沿y负方向运动,因此粒子a与b速度方向的夹角就是粒子a与y负方向的夹角
![]()
因此夹角
![]()

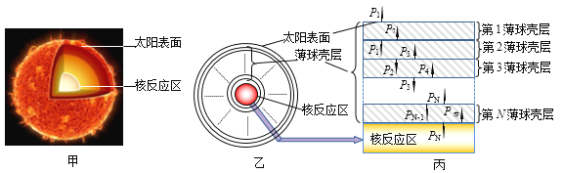
【题目】为测量某金属丝的电阻率,小明同学设计了如图甲、乙所示的两种实验方案,已知电源的电动势E和内阻r在实验过程中保持不变。
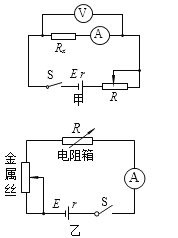
(1)小明先进行了如图甲方案的测量。
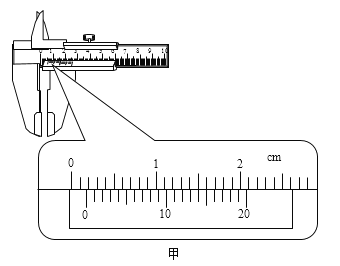
①他首先利用游标卡尺和螺旋测微器分别测出甲、乙、丙三根不同金属丝的直径,示数分别如图甲、乙、丙所示。则三根金属丝直径的测量值分别为d甲=________mm、d乙=________mm、d丙=________mm。若三根金属丝的材料、长度相同且粗细均匀,则它们的电阻R甲、R乙和R丙中最大的是________,最小的是________。

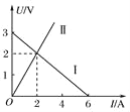
②实验过程中,小明先将甲金属丝接入电路,并用米尺测出接入电路中的甲金属丝的长度l=50.00cm。闭合开关后移动滑动变阻器的滑片分别处于不同的位置,并依次记录了两电表的测量数据如下表所示,其中5组数据的对应点他已经标在如图所示的坐标纸上,请你标出余下一组数据的对应点,并画出U-I图线________________。
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
U/V | 0.90 | 1.20 | 1.50 | 1.80 | 2.10 | 2.40 |
I/A | 0.18 | 0.24 | 0.31 | 0.37 | 0.43 | 0.49 |
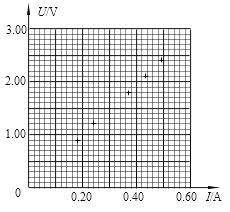
③该方案测得的甲金属丝的电阻率ρ甲=__________Ω·m(计算结果保留两位有效数字)。
④对于上述第(1)所述的测量过程,随着通过金属丝的电流I不断增大,滑动变阻器上的电功率P随之变化。对于P-I的关系图象,在下列图中可能正确的是(________)

(2)小明又用如图乙方案测量乙金属丝的电阻率,已知电源的电动势E=5.0V、内阻r=0.20Ω。实验中他可以通过改变接线夹(即图乙中滑动变阻器符号上的箭头)接触金属丝的位置以控制接入电路中金属丝的长度。
①请在下述步骤的空格中将实验操作步骤补充完整:
a.正确连接电路,设定电阻箱的阻值,闭合开关;
b.读出电流表的示数,记录接线夹的位置;
c.断开开关,______________;
d.闭合开关,重复b、c的操作。
②根据测得电流与金属丝接入长度关系的数据,绘出如图所示的关系图线,其斜率为_____________A-1m-1(保留2位有效数字);图线纵轴截距与电源电动势的乘积代表了___________________的电阻之和。

③图中图线的斜率、电源电动势和金属丝横截面积的乘积代表的物理量是____________,其数值和单位为_______________(保留2位有效数字)。
(3)电表的内阻可能对实验产生系统误差,请你分别就这两种方案说明电表内阻对电阻率测量的影响____________________________________。