��Ŀ����
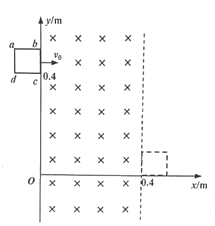
����Ŀ����ͼ��ʾ������ֱƽ���ڽ���xOy����ϵ����O��x��0.4��Χ�ڴ���һ��������߽磬�Ÿ�Ӧǿ�ȴ�СΪ0.1T������ֱֽ���������ǿ�ų�����һ�߳�L=0.10m������m=0.02kg�����������θ��Ե��߿�abcd����ͼʾλ��[c�������Ϊ��0��0.4m��]�Գ��ٶ�v0=2.0m/sˮƽ�����׳������߿�պ�ȫ���뿪�ų�ʱ���±߽�ǡ�õ���x�ᣬ����ˮƽ�ٶ�Ϊ���߿���ȫ������ʼ�մ���xOyƽ���ڣ���ab����x�ᱣ��ƽ�У������������ơ���
(1)�߿�ս���ų�ʱad������Ʋ�uad�Ĵ�С�����ж�a��d������Ƶĸߵͣ�
(2)�߿��±߽�յ���x��ʱ���ٶȺ���ȫ�����в����Ľ�����Q��
(3)����֪���߿����ų������У�ad������Ʋ�uad��ˮƽλ��x�ĺ�����ϵΪ��uad=u0-kx��ʽ��u0��k��Ϊ�����������߿�����ͨ��x=0.2mλ��ʱˮƽ������ٶȡ�
���𰸡���1��![]() ��a����Ƹߣ���2��Q=0.04J����3��
��a����Ƹߣ���2��Q=0.04J����3��![]()
��������
(1)�������ֶ����֪��a����Ƹߣ�
![]()
![]()
(2)�߿���ֱ���������СΪmg
![]()
![]()
�������غ�
![]()
��
Q=0.04J
(3)��Ϊ�߿��ڽ���ų�ʱuad=u0-kx���ɵ��ٶȱ仯����ˮƽλ�Ƴ����ȡ�
ͬ���ɵ��߿����뿪�ų�ʱ���ٶȱ仯��Ҳ��ˮƽλ�Ƴ����ȣ�Ҳ���ù�ʽ������
![]()