��Ŀ����
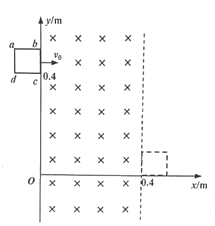
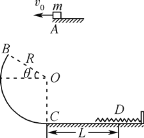
����Ŀ����ͼ��ʾ���뾶R��0.4m�Ĺ⻬Բ�����BC�̶�����ֱƽ���ڣ�������϶˵�B��Բ��O��������ˮƽ����ļн�����30�����¶˵�CΪ�������͵�����ֲ�ˮƽ�����У�һ�����ʵ��ɵ��Ҷ˹̶�����ֱ�����ϣ�����m��0.1kg��С���(����Ϊ�ʵ�)�ӿ��е�A����v0��2m/s���ٶȱ�ˮƽ������ǡ�ô�B���ع�����߷��������������C�����ˮƽ�������˶���D��ʱ�����ɱ�ѹ������̣���ʱ���ɵĵ�������Epm��0.8J����֪С�����ˮƽ���Ķ�Ħ����������0.5��ȡg��10m/s2����
��1��С����A���˶���B���ʱ�䣻
��2��С��龭��Բ������ϵ�C��ʱ���Թ����ѹ����С��
��3��C��D������ˮƽ����L��
���𰸡�(1) ![]() (2) 8N (3) 1.2m
(2) 8N (3) 1.2m
��������
(1)С���ǡ�ô�B�������߷�����������ٶ�����ֱ����ļнǵ��������ɼ��ι�ϵ�У�![]()
��ã�
![]()
(2)��B��C���̣��ɶ��ܶ����ã�![]()
��B�㣬�У�![]()
��C������ţ�ٵڶ������У�FN��mg��![]()
��ã�
FN��8N
����ţ�ٵ������ɣ�֪С��龭��Բ�������C��ʱ�Թ����ѹ��Ϊ��FN����FN��8N����������
(3)��C��D���̣��������غ㶨�ɵã���mgL+Epm��![]()
��ã�
L��1.2m

��ϰ��ϵ�д�
�����Ŀ