Question

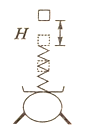
【题目】如图所示，竖直面内半径r=0.8m的1/4圆周的光滑曲面EM与粗糙水平面MN相切于M点，MN长x＝6.0m．过M点的竖直虚线PQ及右侧空间存在水平向里的匀强磁场，B=5T，水平面的右端N处紧邻一半径R（R未知）的绝缘圆筒（图示为圆筒的横截面），圆筒内除了磁场外还有一竖直方向的匀强电场，圆筒上两小孔N、S和圆心O2在水平直径上．水平面上紧邻M点处有一质量m=0.1kg不带电的小球b，另有一个与b完全相同的、带电量q＝–0.01C的小球a从曲面的顶端E处由静止释放，滑到M点处与静止的小球b正碰并粘在一起，碰后的瞬间给粘合体c一个水平推力F，粘合体以a＝1m/s2加速度匀加速运动到N点，同时撤去水平推力，粘合体从N点进入圆筒后作竖直面内的圆周运动．不计空气阻力，小球a、b和粘合体c均视为质点，碰撞前后电荷总量保持不变，粘合体c与水平面间MN间的动摩擦因数μ＝0.5．g取10m/s2．求：

(1)小球a与b碰前瞬间过曲面M点时对M点的压力；

(2)整个过程中水平力F对粘合体c的冲量；

(3)粘合体c从N点进入圆筒后，假设与筒壁碰后速度大小不变，方向反向，若粘合体c与筒壁发生3次碰撞后从S点射出，求圆筒的半径．（已知tan22.5＝）

Answer 1

【答案】(1)3N (2) 2.55N·s (3)m或m

【解析】(1) 小球从E点到M点的过程，由机械能守恒定律得

小球a做圆周运动过M 点时，由牛顿运动定律得

解得：v0＝4m/s，N=3.2N

所以小球a与b碰前瞬间作圆周运动过M点时对M点的压力为3N；

(2) 小球a与小球b碰撞，由动量守恒定律得：mv0＝2mv

解得 v＝2 m/s

粘合体c从M到N的过程，由运动学公式得 和

解得 4m/s，t＝2s

由牛顿运动定律有

代入数据整理得

水平力的冲量；

(3) 若粒子进入磁场后，与筒壁发生三次碰撞后从S点射出有两种情况：

①轨迹如图甲所示

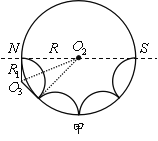
则粒子在磁场中做圆周运动的轨迹半径

根据

解得：

②轨道如图乙所示

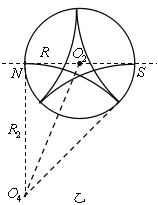
则粒子在磁场中做圆周运动的轨迹半径

根据

解得：。