题目内容
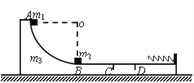
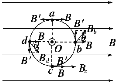
【题目】如图所示，一根通电直导线垂直放在磁感应强度B＝1 T水平向右的匀强磁场中，以导线截面的中心为圆心，半径为r的圆周上有a、b、c、d四点，已知a点的实际磁感应强度为零，则b、c、d三点的磁感应强度分别是多少？方向如何？
【答案】Bb＝
T，与水平方向成45°斜向右上方
Bc＝2 T，方向水平向右
Bd＝ T，与水平方向成45°斜向右下方
【解析】a、b、c、d各点的磁场均为匀强磁场与电流的磁场的叠加，并且电流在这四点所产生的磁感应强度B′大小相等，由于Ba＝0，则B′＝B＝1 T，则由安培定则可知，导线中电流方向向外，则在b、c、d点电流的磁场的磁感应强度如图所示。
Bb＝B＝ T，θ＝45°，即Bb与水平方向成45°角斜向右上方
Bc＝B′＋B＝2 T，方向水平向右
Bd＝B＝ T，α＝45°，即Bd与水平方向成45°角斜向右下方
练习册系列答案
相关题目
