题目内容
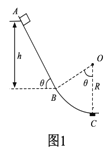
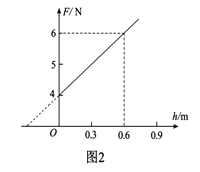
【题目】某小组在研究物体的运动时设计了如图1所示的固定轨道ABC,其中AB部分为粗糙斜面,斜面倾角θ=60°,BC部分为光滑的、圆心角θ=60° 的圆轨道, AB与BC相切于B点,圆轨道的最低点C端下面装有一压力传感器.该小组让小滑块从斜面上不同位置由静止下滑,并记录小滑块起始位置离B点的高度h,小滑块每次刚到达C点时压力传感器的示数F与h的关系图象如图2所示,已知小滑块与斜面之间的动摩擦因数μ=![]() ,重力加速度g=10 m/s2.求:
,重力加速度g=10 m/s2.求:
(1)小滑块沿AB面下滑时的加速度大小a;
(2)小滑块的质量m和圆轨道的半径R.
【答案】(1)a=![]() m/s2 (2)m=0.2 kg R=0.8 m
m/s2 (2)m=0.2 kg R=0.8 m
【解析】
(1)小滑块沿AB面下滑时所受的合外力: ![]()
由牛顿第二定律![]() ,
,
得: ![]()
(2)设小滑块每次刚到达C点时的速度大小为![]() ,由A到C根据动能定理得:
,由A到C根据动能定理得:
![]()
在C点由牛顿第二定律得:F–mg=m![]()
可得:F=![]()
由图2可得:2mg=4,![]()
解得:m=0.2 kg,R=0.8 m

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目