题目内容
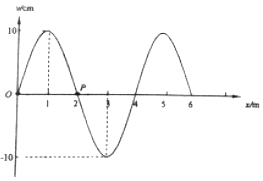
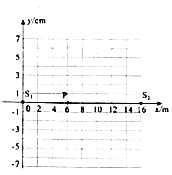
【题目】如图所示,两列简谐横波分别从x轴上的x1=0、x2=16m处相向传播,波长均为λ=8m,t=0时两波源S1和S2沿y轴正方向振动,方程分别为y1=4sin(![]() t)cm和y2=3sin(
t)cm和y2=3sin(![]() t)cm.求:
t)cm.求:
①波源S1产生的简谐横波的周期与波速;
②t=6s时S1和S2之间波形图中位移最大点的位置以及此时P点的位移。
【答案】:①波源S1产生的简谐横波的周期为4s,波速为2m/s。
②t=6s时S1和S2之间波形图中位移最大点的位置为x=4m、8m、12m。此时P点的位移为-1cm。
【解析】
考查简谐振动、波的传播规律,根据振动和波动规律分析可得。
①分析振动方程可知,圆频率ω=![]() rad/s,则周期T=
rad/s,则周期T=![]() =4s。
=4s。
根据波长、波速和周期的关系可知,波速v=![]() =2m/s。
=2m/s。
②波速为2m/s,t=6s时,两波均传播了12m,即波S1和传播到x=12m处,波S2传播到x=4m处,则叠加部分为4m~12m之间。
两波振动频率相同,根据干涉条件可知,振动加强点满足波程差等于整数个波长,△x=nλ。
当n=0时,△x=0,该位置为x=8m处;
当n=1时,△x=λ,该位置为x=4m、x=12m处。
P点的波程差为4m,为半波长的奇数倍,振动减弱点,t=6s时的位移为-1cm。
答:①波源S1产生的简谐横波的周期为4s,波速为2m/s。
②t=6s时S1和S2之间波形图中位移最大点的位置为x=4m、8m、12m。此时P点的位移为-1cm。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目