Question

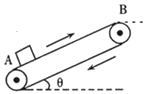
【题目】如图所示，传送带与水平面的夹角θ=30°，正以恒定的速度v=2.5m/s顺时针转动，现在其底端A轻放一货物（可视为质点），货物与传送带间的动摩擦因数μ=，经过t=2s，传送带突然被卡住而立即停止转动，由于惯性，货物继续沿传送带向上运动，并刚好到达传送带顶端B．求传送带底端A与顶端B的距离．（g取10m/s2）

Answer 1

【答案】4m

【解析】货物从A处开始做匀加速运动，设加速度为a1，由牛顿第二定律得
μmgcosθ-mgsinθ=ma1
代入数据得 a1=2.5m/s2
匀加速运动的时间

位移

在t=1-2s内，货物随传送带一起匀速的位移为x2=v（t-t1）=2.5×（2-1）=2.5m
传送带停止转动后，货物匀减速运动到B端，速度刚好为0．设加速度大小为a2。
所以μmgcosθ+mgsinθ=ma2
代入数据得 a2=12.5m/s2
匀减速的位移为 x3==0.25m
则传送带底端A与顶端B的距离 L=x1+x2+x3=4m