题目内容
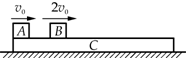 (2007?岳阳模拟)如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ.最初木板静止,A、B两木块同时以方向水平向右的初速度v0和2v0在木板上滑动,木板足够长,A、B始终未滑离木板.求:
(2007?岳阳模拟)如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ.最初木板静止,A、B两木块同时以方向水平向右的初速度v0和2v0在木板上滑动,木板足够长,A、B始终未滑离木板.求:(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移;
(2)木块A在整个过程中的最小速度.
分析:(1)A、B两木块同时水平向右滑动后,木块A先做匀减速直线运动,当木块A与木板C的速度相等后,A、C相对静止一起在C摩擦力的作用下做匀加速直线运动;木块B一直做匀减速直线运动,直到三个物体速度相同.根据三个物体组成的系统动量守恒求出最终共同的速度,对B由牛顿第二定律和运动学公式或动能定理求解发生的位移;
(2)当木块A与木板C的速度相等时,木块A的速度最小,根据系统的动量守恒求解A在整个过程中的最小速度,或根据牛顿第二定律分别研究A、C,求出加速度,根据速度公式,由速度相等条件求出时间,再求解木块A在整个过程中的最小速度.
(2)当木块A与木板C的速度相等时,木块A的速度最小,根据系统的动量守恒求解A在整个过程中的最小速度,或根据牛顿第二定律分别研究A、C,求出加速度,根据速度公式,由速度相等条件求出时间,再求解木块A在整个过程中的最小速度.
解答:解:(1)木块A先做匀减速直线运动,后做匀加速直线运动;木块B一直做匀减速直线运动;木板C做两段加速度不同的匀加速直线运动,直到A、B、C三者的速度相等为止,设为v1.对A、B、C三者组成的系统,由动量守恒定律得:
mv0+2mv0=(m+m+3m)v1
解得:v1=0.6v0
木块B滑动的加速度为:a=μg,
所发生的位移:x=
=
(2)A与C速度相等时,速度最小,此过程A和B减少的速度相等,有:
mv0+2mv0=(m+3m)vA+mvB
v0-vA=2v0-vB
解得:vA=0.4v0
答:(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移是
;
(2)木块A在整个过程中的最小速度是0.4v0.
mv0+2mv0=(m+m+3m)v1
解得:v1=0.6v0
木块B滑动的加速度为:a=μg,
所发生的位移:x=
| ||
| -2a |
91
| ||
| 50μg |
(2)A与C速度相等时,速度最小,此过程A和B减少的速度相等,有:
mv0+2mv0=(m+3m)vA+mvB
v0-vA=2v0-vB
解得:vA=0.4v0
答:(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移是
91
| ||
| 50μg |
(2)木块A在整个过程中的最小速度是0.4v0.
点评:本题是木块在木板上滑动的类型,分析物体的运动过程是解题基础,其次要把握物理过程所遵守的规律,这种类型常常根据动量守恒和能量守恒结合处理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

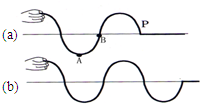 (2007?岳阳模拟)如图(a) 所示,用手拿着绳子的一端上下摆动,保持摆动幅度相等,就会看到一列凹凸相间的波向绳子的另一端传去.设在t时刻波传到P点,则下列判断错误的是
(2007?岳阳模拟)如图(a) 所示,用手拿着绳子的一端上下摆动,保持摆动幅度相等,就会看到一列凹凸相间的波向绳子的另一端传去.设在t时刻波传到P点,则下列判断错误的是 (2007?岳阳模拟)S1、S2是两个振动频率相同的波源,它们发出两列波长均为λ 的简谐横波,图中虚线和实线分别代表某时刻这两列波的波谷和波峰,
(2007?岳阳模拟)S1、S2是两个振动频率相同的波源,它们发出两列波长均为λ 的简谐横波,图中虚线和实线分别代表某时刻这两列波的波谷和波峰, (2007?岳阳模拟)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm.在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5.5s时,观察者看到B处恰好第三次出现波谷,下列判断错误的是( )
(2007?岳阳模拟)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm.在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5.5s时,观察者看到B处恰好第三次出现波谷,下列判断错误的是( )