题目内容
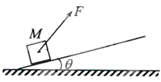
【题目】如图所示,一质量为mB=2 kg,长为L=6 m的薄木板B放在水平面上,质量为mA=2 kg的物体A(可视为质点)在一电动机拉动下从木板左端以v0=5 m/s的速度向右匀速运动。在物体带动下,木板以a=2 m/s2的加速度从静止开始做匀加速直线运动,此时牵引物体的轻绳的拉力F=8 N。已知各接触面间的动摩擦因数恒定,重力加速度g取10 m/s2,则
![]()
(1)经多长时间物体A滑离木板?
(2)木板与水平面间的动摩擦因数为多少?
【答案】(1) 2 s(2) 0.1
【解析】
(1) 当物块刚好滑落时,在运动过程中分别求出两物体的位移,两位移之差等于木板的长度,即可求得;
(2) 利用牛顿第二定律求出地面对物体的摩擦力,由滑动摩擦力公式求的摩擦因数。
(1) 设经t0时间物体A滑离木板,则对A:SA=v0t0
对木板B:![]()
SA-SB=L
联立解得:t0=2s,t′=3s(舍去);
(2) AB间的滑动摩擦力为:fAB=F=8N
此时地面对B的摩擦力满足:fAB-f=mBa
解得:f=4N
地面对B的摩擦力:f=μFN,FN=(mA+mB)g=40N
联立解得:μ=0.1。

练习册系列答案
相关题目