ћвƒњƒЏ»Ё
”о÷ж÷–іж‘Џ“ї–©јл∆дЋьЇг–«љѕ‘ґµƒ°Ґ”…÷ Ѕњѕаµ»µƒ»эњ≈–«„й≥…µƒ»э–« ѕµЌ≥£ђЌ®≥£њ…Їц¬‘∆дЋь–«ћеґ‘Ћь√«µƒ“эЅ¶„ч”√£Ѓ“—єџ≤вµљќ»ґ®µƒ»э–«ѕµЌ≥іж‘ЏЅљ÷÷їщ±Њµƒєє≥…–ќ љ£Ї“ї÷÷ «»эњ≈–«ќї”ЏЌђ“ї÷±ѕя…ѕ£ђЅљњ≈–«ќІ»∆÷–—л–«‘ЏЌђ“ї∞лЊґќ™Rµƒ‘≤ємµј…ѕ‘Ћ––£їЅн“ї÷÷–ќ љ «»эњ≈–«ќї”Џµ»±я»эљ«–ќµƒ»эЄцѕоµг…ѕ£ђ≤Ґ—ЎЌвљ””Џµ»±я»эљ«–ќµƒ‘≤–ќємµј‘Ћ––£Ѓ…и√њЄц–«ћеµƒ÷ ЅњЊщќ™m£ЃµЏ“ї÷÷–ќ љѕ¬£ђ–«ће‘ЋґѓµƒѕяЋўґ»ќ™
£ђ÷№∆Џќ™
R
R£Ѓ
|
|
4¶–R
£Ѓ
|
4¶–R
£Ѓ
£ЃЉў…иЅљ÷÷–ќ љ–«ћеµƒ‘Ћґѓ÷№∆ЏѕаЌђ£ђµЏґю÷÷–ќ љѕ¬–«ће÷ЃЉдµƒЊајл”¶ќ™
|
| 3 |
| ||
| 3 |
| ||
Ј÷ќц£Ї√ч»Ј—–Њњґ‘ѕу£ђґ‘—–Њњґ‘ѕу №Ѕ¶Ј÷ќц£ђ’“µљ„ц‘≤÷№‘ЋґѓЋщ–иѕт–ƒЅ¶µƒјі‘і£Ѓ
љвір£Їљв£Ї£®1£©‘ЏµЏ“ї÷÷–ќ љѕ¬£Ї»эњ≈–«ќї”ЏЌђ“ї÷±ѕя…ѕ£ђЅљњ≈–«ќІ»∆÷–—л–«‘ЏЌђ“ї∞лЊґќ™Rµƒ‘≤ємµј…ѕ‘Ћ––£ї
∆д÷–±я…ѕµƒ“їњ≈–« №÷–—л–«ЇЌЅн“їњ≈±я…ѕ–«µƒЌт”–“эЅ¶ћбє©ѕт–ƒЅ¶£Ѓ
G
+G
=m
љв÷Ѓµ√£Їv=
T=
=4¶–R
Ґў
£®2£©Ѕн“ї÷÷–ќ љ «»эњ≈–«ќї”Џµ»±я»эљ«–ќµƒ»эЄцѕоµг…ѕ£ђ≤Ґ—ЎЌвљ””Џµ»±я»эљ«–ќµƒ‘≤–ќємµј‘Ћ––£ђ
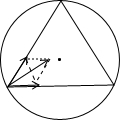
”…Ќт”–“эЅ¶ґ®¬…ЇЌ≈£ґўµЏґюґ®¬…µ√£Ї2
cos30°г=m
(
)2 ҐЏ
”–ҐўҐЏљвµ√£ЇL=
R
є ір∞Єќ™£Ї
£ї4¶–R
£ї
R
∆д÷–±я…ѕµƒ“їњ≈–« №÷–—л–«ЇЌЅн“їњ≈±я…ѕ–«µƒЌт”–“эЅ¶ћбє©ѕт–ƒЅ¶£Ѓ
G
| m2 |
| R2 |
| m2 |
| (2R)2 |
| v2 |
| R |
љв÷Ѓµ√£Їv=
|
T=
| 2¶–R |
| v |
|
£®2£©Ѕн“ї÷÷–ќ љ «»эњ≈–«ќї”Џµ»±я»эљ«–ќµƒ»эЄцѕоµг…ѕ£ђ≤Ґ—ЎЌвљ””Џµ»±я»эљ«–ќµƒ‘≤–ќємµј‘Ћ––£ђ

”…Ќт”–“эЅ¶ґ®¬…ЇЌ≈£ґўµЏґюґ®¬…µ√£Ї2
| Gm2 |
| L2 |
| L |
| 2cos30°г |
| 2¶– |
| T |
”–ҐўҐЏљвµ√£ЇL=
| 3 |
| ||
є ір∞Єќ™£Ї
|
|
| 3 |
| ||
µг∆ј£ЇЌт”–“эЅ¶ґ®¬…ЇЌ≈£ґўµЏґюґ®¬… «Ѕ¶—Іµƒ÷Ўµг£ђ‘Џ±Њћв÷–”––©Ќђ—І’“≤ї≥ц ≤√іЅ¶ћбє©ѕт–ƒЅ¶£ђєЎЉь‘Џ”Џљш––’э»Ј №Ѕ¶Ј÷ќц£Ѓ

ЅЈѕ∞≤бѕµЅ–ір∞Є
 Њў“їЈі»э∆Џƒ©∞ўЈ÷≥еіћЊнѕµЅ–ір∞Є
Њў“їЈі»э∆Џƒ©∞ўЈ÷≥еіћЊнѕµЅ–ір∞Є
ѕаєЎћвƒњ
 ”о÷ж÷–іж‘Џ“ї–©јл∆дЋьЇг–«Ї№‘ґµƒЋƒњ≈Їг–«„й≥…µƒЋƒ–«ѕµЌ≥£ђЌ®≥£њ…Їц¬‘∆дЋь–«ћеґ‘Ћь√«µƒ“эЅ¶„ч”√£Ѓќ»ґ®µƒЋƒ–«ѕµЌ≥іж‘Џґа÷÷–ќ љ£ђ∆д÷–“ї÷÷ «Ћƒњ≈÷ Ѕњѕаµ»µƒЇг–«ќї”Џ’эЈљ–ќµƒЋƒЄцґ•µг…ѕ£ђ—Ў„≈Ќвљ””Џ’эЈљ–ќµƒ‘≤–ќємµј„ц‘»Ћў‘≤÷№‘Ћґѓ£їЅн“ї÷÷»зЌЉЋщ Њ£ђЋƒњ≈Їг–« Љ÷’ќї”ЏЌђ“ї÷±ѕя…ѕ£ђЊщќІ»∆÷–µгO„ц‘»Ћў‘≤÷№‘Ћґѓ£Ѓ“—÷™Ќт”–“эЅ¶≥£Ѕњќ™G£ђ«у£Ї
”о÷ж÷–іж‘Џ“ї–©јл∆дЋьЇг–«Ї№‘ґµƒЋƒњ≈Їг–«„й≥…µƒЋƒ–«ѕµЌ≥£ђЌ®≥£њ…Їц¬‘∆дЋь–«ћеґ‘Ћь√«µƒ“эЅ¶„ч”√£Ѓќ»ґ®µƒЋƒ–«ѕµЌ≥іж‘Џґа÷÷–ќ љ£ђ∆д÷–“ї÷÷ «Ћƒњ≈÷ Ѕњѕаµ»µƒЇг–«ќї”Џ’эЈљ–ќµƒЋƒЄцґ•µг…ѕ£ђ—Ў„≈Ќвљ””Џ’эЈљ–ќµƒ‘≤–ќємµј„ц‘»Ћў‘≤÷№‘Ћґѓ£їЅн“ї÷÷»зЌЉЋщ Њ£ђЋƒњ≈Їг–« Љ÷’ќї”ЏЌђ“ї÷±ѕя…ѕ£ђЊщќІ»∆÷–µгO„ц‘»Ћў‘≤÷№‘Ћґѓ£Ѓ“—÷™Ќт”–“эЅ¶≥£Ѕњќ™G£ђ«у£Ї